
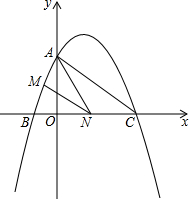
 如圖,已知二次函數y=ax2+$\frac{3}{2}$x+c的圖象與y軸交于點A(0,4),與x軸交于點B,C,點C的坐標為(8,0),連接AC、AC.
如圖,已知二次函數y=ax2+$\frac{3}{2}$x+c的圖象與y軸交于點A(0,4),與x軸交于點B,C,點C的坐標為(8,0),連接AC、AC.分析 (1)將點A和點C的坐標代入代入拋物線的解析式,求得a,c的值即可;
(2)先求得點B的坐標,從而得到BC=10,然后依據勾股定理可求得AB2、AC2的值,最后依據勾股定理的逆定理進行判斷即可;
(3)設點N的坐標為(n,0)(-2<n<8),則BN=n+2,CN=8-n,利用平行線分線段成比例定理可得到$\frac{AM}{AB}$=$\frac{NC}{BC}$=$\frac{8-n}{10}$,然后依據等高的兩個三角形的面積比等于底邊的長度比可得到S△AMN與n的函數關系式,最后利用二次函數的性質可求得△AMN的面積取得最大值時點N的坐標.
解答 解:(1)將點A和點C的坐標代入得:$\left\{\begin{array}{l}{c=4}\\{64a+12+c=0}\end{array}\right.$,
解得:a=-$\frac{1}{4}$,c=4.
∴該二次函數的解析式為y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4.
(2)令y=0得:-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0,解得:x=-2或x=8,
∴點B(-2,0).
∴BC=10.
在Rt△AOB和Rt△AOC中,依據勾股定理可知:AB2=OB2+AO2=20,AC2=OA2+OC2=80,
∴AB2+AC2=BC2.
∴△ABC為直角三角形.
(3)設點N的坐標為(n,0)(-2<n<8),則BN=n+2,CN=8-n.
∵MN∥AC,
∴$\frac{AM}{AB}$=$\frac{NC}{BC}$=$\frac{8-n}{10}$.
∵AO=4,BC=10,
∴S△ABC=$\frac{1}{2}$BC•AO=$\frac{1}{2}$×4×10=20.
∴S△ABN=$\frac{n+2}{10}$S△ABC=2(n+2).
∴S△AMN=$\frac{8-n}{10}$S△AMN=$\frac{1}{5}$(8-n)(n+2)=-$\frac{1}{5}$(n-3)2+5.
∴當n=3時,即N(3,0)時,△AMN的面積最大,最大值為5.
點評 本題主要考查的是二次函數函數的綜合應用,解答本題主要應用了勾股定理、勾股定理的逆定理、平行線分線段成比例定理,列出△AMN的面積與點N的橫坐標n之間的關系式是解題的關鍵.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:解答題
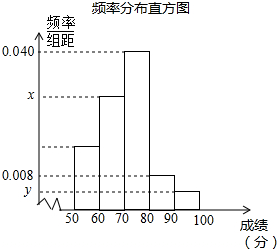 為參加學校的“我愛古詩詞”知識競賽,小王所在班級組織了一次古詩詞知識測試,并將全班同學的分數(得分取正整數,滿分為100分)進行統計,以下是根據這次測試成績制作的不完整的頻率分布表和頻率分布直方圖.
為參加學校的“我愛古詩詞”知識競賽,小王所在班級組織了一次古詩詞知識測試,并將全班同學的分數(得分取正整數,滿分為100分)進行統計,以下是根據這次測試成績制作的不完整的頻率分布表和頻率分布直方圖. | 組別 | 分組 | 頻數 | 頻率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | |
| 3 | 70≤x<80 | 20 | 0.40 |
| 4 | 80≤x<90 | 0.08 | |
| 5 | 90≤x≤100 | 2 | b |
| 合計 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
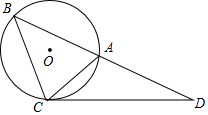 如圖所示,△ABC的外接圓⊙O的半徑為2,過點C作∠ACD=∠ABC,交BA的延長線于點D,若∠ABC=45°,∠D=30°.
如圖所示,△ABC的外接圓⊙O的半徑為2,過點C作∠ACD=∠ABC,交BA的延長線于點D,若∠ABC=45°,∠D=30°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
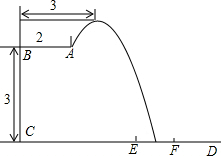 2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.
2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com