
| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
分析 根據關于x的函數y=(1-m)x2+2x+1的圖象與x軸至少有一個交點可分兩種情況進行討論,一種是此函數為一次函數,一種是此函數為二次函數,從而可以解答本題.
解答 解:∵關于x的函數y=(1-m)x2+2x+1的圖象與x軸至少有一個交點,
∴當1-m=0,即m=1時,函數y=2x+1為一次函數,其解析式為y=2x+1,過一、二、三象限,與x軸只有一個交點;
當1-m≠0,即m≠1時,函數y=(1-m)x2+2x+1為二次函數,
△=22-4(1-m)≥0,
解得,m≥0.
由上可得,m的值為不小于零的數,
∴m的值不可能是-1,
故選C.
點評 本題考查了命題與定理、拋物線與x軸的交點、一次函數圖象上點的坐標特征,解答本題的關鍵是明確題意,利用分類討論的數學思想解答,難度不大,注意圖象與x軸至少有一個交點.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:解答題
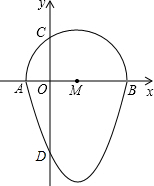 如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.
如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
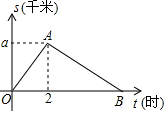 某單位舉行“健康人生”徒步走活動,某人從起點體育村沿建設路到市生態園,再沿原路返回,設此人離開起點的路程s(千米)與走步時間t(小時)之間的函數關系如圖所示,其中從起點到市生態園的平均速度是4千米/小時,用2小時,根據圖象提供信息,解答下列問題.
某單位舉行“健康人生”徒步走活動,某人從起點體育村沿建設路到市生態園,再沿原路返回,設此人離開起點的路程s(千米)與走步時間t(小時)之間的函數關系如圖所示,其中從起點到市生態園的平均速度是4千米/小時,用2小時,根據圖象提供信息,解答下列問題.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
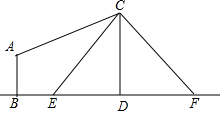 如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=$\sqrt{3}$米,BE=3米,求拉線CE的長.
如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=$\sqrt{3}$米,BE=3米,求拉線CE的長.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com