
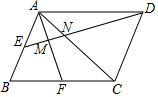
 如圖,點E,F(xiàn)分別是?ABCD兩邊AB、BC的中點,且AF、AC分別與ED交于M、N兩點,有下列結(jié)論:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分點;④△AMN~△DMA.其中正確的是:①③.(把所有正確結(jié)論的序號都選上)
如圖,點E,F(xiàn)分別是?ABCD兩邊AB、BC的中點,且AF、AC分別與ED交于M、N兩點,有下列結(jié)論:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分點;④△AMN~△DMA.其中正確的是:①③.(把所有正確結(jié)論的序號都選上) 分析 如圖1中,延長DC交AF于H.與△ABF≌△CHF,推出AB=CF=CD,由AE=EB,AE∥DH,推出$\frac{EM}{MD}$=$\frac{AE}{DH}$=$\frac{1}{4}$,$\frac{EN}{DN}$=$\frac{AE}{CD}$=$\frac{1}{2}$,設(shè)EM=a,則DM=4a,EN=$\frac{5}{3}$a,DN=$\frac{10}{3}$a,MN=$\frac{2}{3}$a,可得EM:MN=3:2,MN:DN=1:5,EN:DN=1:2,推出①③正確,②錯誤,如圖2中,當(dāng)AF⊥BC時,顯然⊥ANM≠∠MAD,∴△AMN與△ADM不相似.故④錯誤.
解答 解:如圖1中,延長DC交AF于H.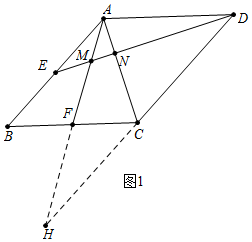
∵四邊形ABCD是平行四邊形,
∴AB∥DH,AB=CD,
∴∠B=∠HCF,
在△ABF和△HCF中,
$\left\{\begin{array}{l}{∠B=∠HCF}\\{FB=CF}\\{∠ABF=∠CFH}\end{array}\right.$,
∴△ABF≌△CHF,
∴AB=CF=CD,
∵AE=EB,AE∥DH,
∴$\frac{EM}{MD}$=$\frac{AE}{DH}$=$\frac{1}{4}$,$\frac{EN}{DN}$=$\frac{AE}{CD}$=$\frac{1}{2}$,設(shè)EM=a,則DM=4a,EN=$\frac{5}{3}$a,DN=$\frac{10}{3}$a,MN=$\frac{2}{3}$a,
∴EM:MN=3:2,MN:DN=1:5,EN:DN=1:2,
∴①③正確,②錯誤,
如圖2中,當(dāng)AF⊥BC時,顯然⊥ANM≠∠MAD,∴△AMN與△ADM不相似.故④錯誤.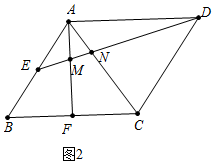
故答案為①③.
點評 本題考查相似三角形的判定和性質(zhì)、平行線的性質(zhì)等知識,解題的關(guān)鍵是學(xué)會添加輔助線,構(gòu)造相似三角形解決問題,屬于中考常考題型.


 智慧課堂密卷100分單元過關(guān)檢測系列答案
智慧課堂密卷100分單元過關(guān)檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
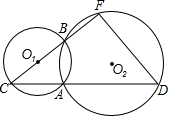 如圖,已知⊙O1與⊙O2交于A,B兩點,點C在⊙O1上且在⊙O2外,CA,CB的延長線分別與⊙O2交于點D,E,AC=3,AD=6,⊙O1的半徑為2.則點O1到DE的距離為 ( )
如圖,已知⊙O1與⊙O2交于A,B兩點,點C在⊙O1上且在⊙O2外,CA,CB的延長線分別與⊙O2交于點D,E,AC=3,AD=6,⊙O1的半徑為2.則點O1到DE的距離為 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
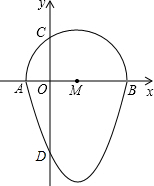 如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標(biāo)軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.
如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標(biāo)軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
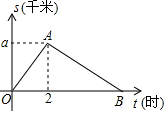 某單位舉行“健康人生”徒步走活動,某人從起點體育村沿建設(shè)路到市生態(tài)園,再沿原路返回,設(shè)此人離開起點的路程s(千米)與走步時間t(小時)之間的函數(shù)關(guān)系如圖所示,其中從起點到市生態(tài)園的平均速度是4千米/小時,用2小時,根據(jù)圖象提供信息,解答下列問題.
某單位舉行“健康人生”徒步走活動,某人從起點體育村沿建設(shè)路到市生態(tài)園,再沿原路返回,設(shè)此人離開起點的路程s(千米)與走步時間t(小時)之間的函數(shù)關(guān)系如圖所示,其中從起點到市生態(tài)園的平均速度是4千米/小時,用2小時,根據(jù)圖象提供信息,解答下列問題.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com