Question

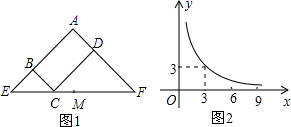
6．圖1所示矩形ABCD中，BC=x，CD=y，y與x滿足的反比例函數關系如圖2所示，等腰直角三角形AEF的斜邊EF過點C，M為EF的中點，則下列結論正確的是（　　）

• A． 當x=3時，EC＜EM
• B． 當x=9時，EC＜EM
• C． 當x增大時，BE•DF的值不變
• D． 當x增大時，EC•CF的值增大

Answer 1

分析 由于等腰直角三角形AEF的斜邊EF過C點，則△BEC和△DCF都是直角三角形；觀察反比例函數圖象得反比例解析式為y=$\frac{9}{x}$；當x=3時，y=3，即BC=CD=3，根據等腰直角三角形的性質得CE=3$\sqrt{2}$，CF=3$\sqrt{2}$，則C點與M點重合；當x=9時，根據反比例函數的解析式得x=1，即BC=9，CD=1，所以EF=10$\sqrt{2}$，而EM=5$\sqrt{2}$；利用等腰直角三角形的性質BE•DF=BC•CD=xy，然后再根據反比例函數的性質得BE•DF=9，其值為定值；由于EC•CF=$\sqrt{2}$x×$\sqrt{2}$y=2xy，其值為定值．

解答 解：因為等腰直角三角形AEF的斜邊EF過C點，M為EF的中點，所以△BEC和△DCF都是直角三角形；觀察反比例函數圖象得x=3，y=3，則反比例解析式為y=$\frac{9}{x}$．
A、當x=3時，y=3，即BC=CD=3，所以CE=$\sqrt{2}$BC=3$\sqrt{2}$，CF=$\sqrt{2}$CD=3$\sqrt{2}$，C點與M點重合，則EC=EM，所以A選項錯誤；
B、當x=9時，y=1，即BC=9，CD=1，所以EC=9$\sqrt{2}$，EF=10$\sqrt{2}$，EM=5$\sqrt{2}$，所以B選項錯誤；
C、因為BE•DF=BC•CD=xy=9，即BE•DF的值不變，所以C選項正確；
D、因為EC•CF=$\sqrt{2}$x•$\sqrt{2}$y=2×xy=18，所以，EC•CF為定值，所以D選項錯誤．
故選C．

點評 本題考查了動點問題的函數圖象：先根據幾何性質得到與動點有關的兩變量之間的函數關系，然后利用函數解析式和函數性質畫出其函數圖象，注意自變量的取值范圍．