
分析 (1)設購進甲型電視機x臺,乙型電視機y臺,丙型電視機z臺,分①只購進甲、乙兩種不同型號的電視機、②只購進甲、丙兩種不同型號的電視機、③只購進乙、丙兩種不同型號的電視機三種情況考慮,根據三種型號電視機的出廠價、購進臺數以及購機的總花費為90000元即可得出二元一次方程組,解方程組后再根據x、y、z均為正整數即可得出結論;
(2)根據總利潤=每臺利潤×購進臺數即可求出各購機方案的利潤,比較后即可得出結論.
解答 解:(1)設購進甲型電視機x臺,乙型電視機y臺,丙型電視機z臺,
①當購進甲、乙兩種不同型號的電視機時,
$\left\{\begin{array}{l}{x+y=50}\\{1500x+2100y=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=25}\\{y=25}\end{array}\right.$;
②當購進甲、丙兩種不同型號的電視機時,
$\left\{\begin{array}{l}{x+z=50}\\{1500x+2500z=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35}\\{z=15}\end{array}\right.$;
③當購進乙、丙兩種不同型號的電視機時,
$\left\{\begin{array}{l}{y+z=50}\\{2100y+2500z=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{y=87.5}\\{z=-37.5}\end{array}\right.$(舍去).
綜上所述:可有兩種進貨方案,方案一:購進甲型電視機25臺、乙型電視機25臺;方案二:購進甲型電視機35臺、丙型電視機15臺.
(2)當選擇方案一時:利潤=150×25+200×25=8750(元);
當選擇方案二時:利潤=150×35+250×15=9000(元).
∵8750<9000,
∴購進甲型電視機35臺、丙型電視機15臺可使銷售時獲利最多.
點評 本題考查了二元一次方程組的應用,根據數量關系列出二元一次方程組是解題的關鍵.


科目:初中數學 來源: 題型:解答題
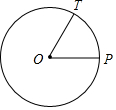 如圖,OP是⊙O的半徑,∠POT=60°,OT交⊙O于點S.
如圖,OP是⊙O的半徑,∠POT=60°,OT交⊙O于點S.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
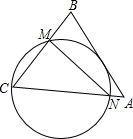 如圖,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,經過點C且與邊AB相切的動圓與CB,CA分別相交于點M,N,則線段MN長度的最小值是3.
如圖,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,經過點C且與邊AB相切的動圓與CB,CA分別相交于點M,N,則線段MN長度的最小值是3.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
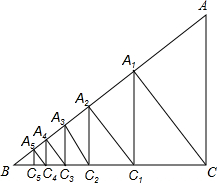 如圖,已知直角△ACB,AC=3,BC=4,過直角頂點C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1;過C1作C1A2⊥AB,垂足為A2,再過A2作A2C2⊥BC,垂足為C2;…,這樣一直做下去,得到一組線段A1C1,A2C2…,則線段AnCn為3×($\frac{4}{5}$)2n.(用含有n的代數式表示)
如圖,已知直角△ACB,AC=3,BC=4,過直角頂點C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1;過C1作C1A2⊥AB,垂足為A2,再過A2作A2C2⊥BC,垂足為C2;…,這樣一直做下去,得到一組線段A1C1,A2C2…,則線段AnCn為3×($\frac{4}{5}$)2n.(用含有n的代數式表示)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
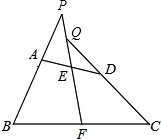 如圖,四邊形ABCD中,已知AB=CD,點E、F分別為AD、BC的中點,延長BA、CD,分別交射線FE于P、Q兩點.求證:∠BPF=∠CQF.
如圖,四邊形ABCD中,已知AB=CD,點E、F分別為AD、BC的中點,延長BA、CD,分別交射線FE于P、Q兩點.求證:∠BPF=∠CQF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
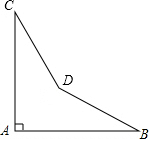 某零件如圖所示,圖紙要求∠A=90°,∠B=32°,∠C=21°,當檢驗員量得∠BDC=145°,就斷定這個零件不合格,你能說出其中的道理嗎?
某零件如圖所示,圖紙要求∠A=90°,∠B=32°,∠C=21°,當檢驗員量得∠BDC=145°,就斷定這個零件不合格,你能說出其中的道理嗎?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
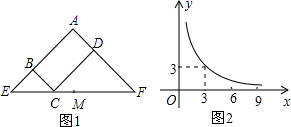 圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數關系如圖2所示,等腰直角三角形AEF的斜邊EF過點C,M為EF的中點,則下列結論正確的是( )
圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數關系如圖2所示,等腰直角三角形AEF的斜邊EF過點C,M為EF的中點,則下列結論正確的是( )| A. | 當x=3時,EC<EM | B. | 當x=9時,EC<EM | ||
| C. | 當x增大時,BE•DF的值不變 | D. | 當x增大時,EC•CF的值增大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com