
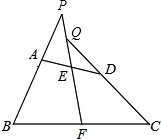
 如圖,四邊形ABCD中,已知AB=CD,點E、F分別為AD、BC的中點,延長BA、CD,分別交射線FE于P、Q兩點.求證:∠BPF=∠CQF.
如圖,四邊形ABCD中,已知AB=CD,點E、F分別為AD、BC的中點,延長BA、CD,分別交射線FE于P、Q兩點.求證:∠BPF=∠CQF. 分析 如圖,連接BD,作BD的中點M,連接FM、EM.利用三角形中位線定理證得△EMF是等腰三角形,則∠MEF=∠MFE.利用三角形中位線定理、平行線的性質推知∠MEF=∠P,∠MFE=∠CQF.根據等量代換證得∠P=∠CQF.
解答 證明:如圖,連接BD,作BD的中點M,連接EM、FM.
∵點E是AD的中點,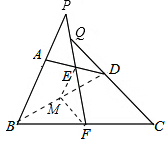
∴在△ABD中,EM∥AB,EM=$\frac{1}{2}$AB,
∴∠MEF=∠P
同理可證:FM∥CD,FM=$\frac{1}{2}$CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF..
點評 此題考查的是三角形中位線的性質、等腰三角形判定和性質等知識,解題的關鍵是題目中出現中點的條件想到添加三角形的中位線作為輔助線,屬于中考常考題型.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 不變 | B. | 擴大到原來的2倍 | C. | 縮小到原來的$\frac{1}{2}$ | D. | 縮小到原來的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (0,5) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com