

分析 (1)根據(jù)等邊三角形的性質(zhì)得到∠ACE=∠DCB=60°,CA=CE,CD=CB,根據(jù)全等三角形的判定定理得到△ECB≌△ACD,根據(jù)全等三角形的性質(zhì)證明;
(2)根據(jù)等邊三角形的性質(zhì)得到∠ACE=∠DCB=60°,CA=CE,CD=CB,根據(jù)全等三角形的判定定理得到△ECB≌△ACD,根據(jù)全等三角形的性質(zhì)證明;
(3)根據(jù)全等三角形的性質(zhì)得到∠BEC=∠DAC,根據(jù)三角形內(nèi)角和定理計(jì)算即可.
解答 解:(1)∵△ACE和△BCD都是等邊三角形,
∴∠ACE=∠DCB=60°,CA=CE,CD=CB,
∴∠ACE+∠DCE=∠DCB+∠DCE,即∠ACD=∠ECB,
在△ECB和△ACD中,
$\left\{\begin{array}{l}{EC=AC}\\{∠ECB=∠ACD}\\{CB=CD}\end{array}\right.$,
∴△ECB≌△ACD,
∴AD=BE,
故答案為:AD=BE;
(2)AD=BE成立.
證明:∵△ACE和△BCD是等邊三角形,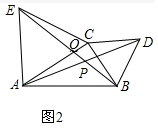
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD,
在△ECB和△ACD中,
$\left\{\begin{array}{l}{EC=AC}\\{∠ECB=∠ACD}\\{CB=CD}\end{array}\right.$,
∴△ECB≌△ACD(SAS),
∴BE=AD;
(3)∠APE不隨著∠ACB的大小發(fā)生變化,始終是60°,
如圖2,設(shè)BE與AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC,
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°,
∴∠APQ=∠ECQ=60°,即∠APE=60°.
點(diǎn)評 本題考查的是等邊三角形的性質(zhì)、全等三角形的判定和性質(zhì),掌握等邊三角形的三條邊相等、三個(gè)角都是60°、全等三角形的判定定理和性質(zhì)定理是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
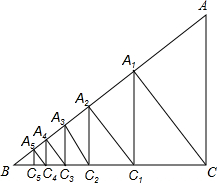 如圖,已知直角△ACB,AC=3,BC=4,過直角頂點(diǎn)C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1;過C1作C1A2⊥AB,垂足為A2,再過A2作A2C2⊥BC,垂足為C2;…,這樣一直做下去,得到一組線段A1C1,A2C2…,則線段AnCn為3×($\frac{4}{5}$)2n.(用含有n的代數(shù)式表示)
如圖,已知直角△ACB,AC=3,BC=4,過直角頂點(diǎn)C作CA1⊥AB,垂足為A1,再過A1作A1C1⊥BC,垂足為C1;過C1作C1A2⊥AB,垂足為A2,再過A2作A2C2⊥BC,垂足為C2;…,這樣一直做下去,得到一組線段A1C1,A2C2…,則線段AnCn為3×($\frac{4}{5}$)2n.(用含有n的代數(shù)式表示)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
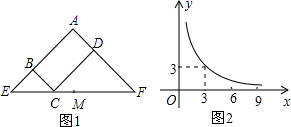 圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數(shù)關(guān)系如圖2所示,等腰直角三角形AEF的斜邊EF過點(diǎn)C,M為EF的中點(diǎn),則下列結(jié)論正確的是( )
圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數(shù)關(guān)系如圖2所示,等腰直角三角形AEF的斜邊EF過點(diǎn)C,M為EF的中點(diǎn),則下列結(jié)論正確的是( )| A. | 當(dāng)x=3時(shí),EC<EM | B. | 當(dāng)x=9時(shí),EC<EM | ||
| C. | 當(dāng)x增大時(shí),BE•DF的值不變 | D. | 當(dāng)x增大時(shí),EC•CF的值增大 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
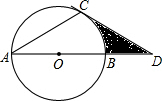 如圖,⊙O的直徑AB為12點(diǎn)D在AB的延長線上,DC切⊙O于點(diǎn)C,且∠DAC=30°,則圖中陰影部分面積為18$\sqrt{3}$-6π.
如圖,⊙O的直徑AB為12點(diǎn)D在AB的延長線上,DC切⊙O于點(diǎn)C,且∠DAC=30°,則圖中陰影部分面積為18$\sqrt{3}$-6π.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3a-a=3 | B. | -(a-b)=-a+b | C. | a+2a2=3a2 | D. | 2(a-1)=2a-1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
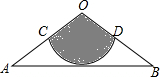 如圖,從一張腰長為60cm,頂角為120°的等腰三角形鐵皮OAB中剪出一個(gè)最大的扇形OCD,用此剪下的扇形鐵皮圍成一個(gè)圓錐的側(cè)面(不計(jì)損耗),則該圓錐的高為20$\sqrt{2}$cm.
如圖,從一張腰長為60cm,頂角為120°的等腰三角形鐵皮OAB中剪出一個(gè)最大的扇形OCD,用此剪下的扇形鐵皮圍成一個(gè)圓錐的側(cè)面(不計(jì)損耗),則該圓錐的高為20$\sqrt{2}$cm.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com