
分析 先證明△BCD∽△BAC,得$\frac{BC}{BA}$=$\frac{BD}{BC}$,設BD=x,可得方程$\frac{12}{x+8}$=$\frac{x}{12}$,求出x即可解決問題.
解答 解:如圖,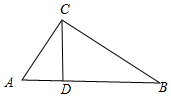
∵CD⊥AB,
∴∠BDC=∠ACB=90°,∵∠B=∠B,
∴△BCD∽△BAC,
∴$\frac{BC}{BA}$=$\frac{BD}{BC}$,
設BD=x,
∴$\frac{12}{x+8}$=$\frac{x}{12}$,
解得x=4$\sqrt{10}$-4或-4$\sqrt{10}$-4(舍棄),
∴AB=AD+BD=8+4$\sqrt{10}$-4=4+4$\sqrt{10}$,
故答案為4+4$\sqrt{10}$.
點評 本題考查相似三角形的判定和性質,解題的關鍵是熟練掌握相似三角形的判定和性質,學會用方程的思想思考問題,屬于中考常考題型.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
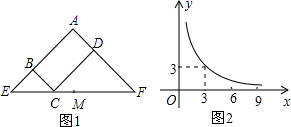 圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數關系如圖2所示,等腰直角三角形AEF的斜邊EF過點C,M為EF的中點,則下列結論正確的是( )
圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數關系如圖2所示,等腰直角三角形AEF的斜邊EF過點C,M為EF的中點,則下列結論正確的是( )| A. | 當x=3時,EC<EM | B. | 當x=9時,EC<EM | ||
| C. | 當x增大時,BE•DF的值不變 | D. | 當x增大時,EC•CF的值增大 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
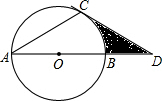 如圖,⊙O的直徑AB為12點D在AB的延長線上,DC切⊙O于點C,且∠DAC=30°,則圖中陰影部分面積為18$\sqrt{3}$-6π.
如圖,⊙O的直徑AB為12點D在AB的延長線上,DC切⊙O于點C,且∠DAC=30°,則圖中陰影部分面積為18$\sqrt{3}$-6π.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com