
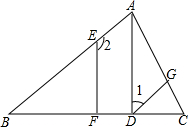
 如圖:已知AD⊥BC于點D,∠1+∠2=180°,∠B=∠CDG,試判斷EF與BC的位置關系并說明理由.
如圖:已知AD⊥BC于點D,∠1+∠2=180°,∠B=∠CDG,試判斷EF與BC的位置關系并說明理由. 分析 先由∠CDG=∠B證明DG∥AB,所以得到∠1=∠DAB,又∠1+∠2=180°,所以∠2+∠DAB=180°,再次推出EF∥AD,即得到∠EFB=∠ADB,已知AD⊥BC于點D,故得到EF與BC的位置關系是垂直.
解答 解:EF與BC的位置關系是垂直關系.
∵∠CDG=∠B(已知),
∴DG∥AB(同位角相等,兩直線平行),
∴∠1=∠DAB(兩直線平行,內錯角相等),
又∠1+∠2=180°(已知),
∴∠2+∠DAB=180°,
∴EF∥AD(內錯角相等,兩直線平行),
∴∠EFB=∠ADB(兩直線平行,同位角相等),
又AD⊥BC于點D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
所以EF與BC的位置關系是垂直.
點評 此題考查的知識點是平行線的判定與性質,關鍵是由已知證明EF∥AD,再證出∠EFB=∠ADB=90°.


科目:初中數學 來源: 題型:填空題
 如圖,四邊形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,點C,E在x軸上,點A在y軸上,點F在雙曲線y=$\frac{k}{x}$(k≠0)第一象限內的圖象上,S△BEF=5,OC=1,則k=8.
如圖,四邊形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,點C,E在x軸上,點A在y軸上,點F在雙曲線y=$\frac{k}{x}$(k≠0)第一象限內的圖象上,S△BEF=5,OC=1,則k=8.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
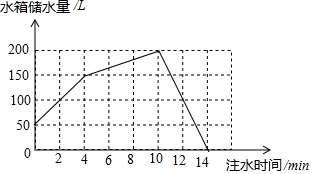 容積為200L的水箱上裝有兩根進水管A,B和一根排水管C.如圖,先由A,B兩根進水管同時向水箱內注水,再由B管單獨向水箱內注水,最后由C管將水箱內的水排完.
容積為200L的水箱上裝有兩根進水管A,B和一根排水管C.如圖,先由A,B兩根進水管同時向水箱內注水,再由B管單獨向水箱內注水,最后由C管將水箱內的水排完.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
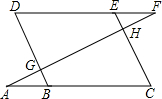 如圖所示,點E在直線DF上,點B在直線AC上,直線AF分別交BD,CE于點G,H.若∠AGB=∠EHF,∠C=∠D,請到斷∠A與∠F的數量關系,并說明理由.
如圖所示,點E在直線DF上,點B在直線AC上,直線AF分別交BD,CE于點G,H.若∠AGB=∠EHF,∠C=∠D,請到斷∠A與∠F的數量關系,并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知△ABC,∠ABC,∠ACB的角平分線交于點O,連接AO并延長交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA長為( )cm.
如圖,已知△ABC,∠ABC,∠ACB的角平分線交于點O,連接AO并延長交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA長為( )cm.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com