
 如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(-1,0),對稱軸為直線x=1,與y軸的交點B在(0,2)和(0,3)之間(包括這兩點),下列結論:①當x>3時,y<0;②a-b+c=0;③-1≤a≤-$\frac{2}{3}$;④4a+2b+c<2;其中正確的結論是( )
如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(-1,0),對稱軸為直線x=1,與y軸的交點B在(0,2)和(0,3)之間(包括這兩點),下列結論:①當x>3時,y<0;②a-b+c=0;③-1≤a≤-$\frac{2}{3}$;④4a+2b+c<2;其中正確的結論是( )| A. | ①③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 ①先由拋物線的對稱性求得拋物線與x軸令一個交點的坐標為(3,0),從而可知當x>3時,y<0;②由拋物線與x軸交于點A(-1,0)可知a-b+c=0,③設拋物線的解析式為y=a(x+1)(x-3),則y=ax2-2ax-3a,令x=0得:y=-3a.由拋物線與y軸的交點B在(0,2)和(0,3)之間,可知2≤-3a≤3.④由拋物線與x軸的交點為(-1,0)和(3,0),且開口向下,根據圖象可知當x=2時,y=4a+2b+c>0.
解答 解:①由拋物線的對稱性可求得拋物線與x軸令一個交點的坐標為(3,0),當x>3時,y<0,故①正確;
②∵二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(-1,0),
∴當x=-1時,y=a-b+c=0,故②正確;
③設拋物線的解析式為y=a(x+1)(x-3),則y=ax2-2ax-3a,
令x=0得:y=-3a.
∵拋物線與y軸的交點B在(0,2)和(0,3)之間,
∴2≤-3a≤3.
解得:-1≤a≤-$\frac{2}{3}$,故③正確;
④∵拋物線與x軸的交點為(-1,0)和(3,0),且開口向下,
∴當x=2時,y=4a+2b+c>0,故④錯誤.
故選:B.
點評 本題主要考查的是二次函數的圖象和性質,掌握拋物線的對稱軸、開口方向與系數a、b、c之間的關系是解題的關鍵.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:選擇題
| A. | 2012(1+x)2=2014 | B. | 2845(1+x)2=3112 | C. | 3112(1+x)2=2845 | D. | 2845(1-x)2=3112 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
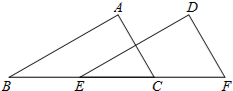 如圖,B,C,E,F四點在一條直線上,AB∥DE,AB=DE,下列條件不能判定△ABC與△DEF全等的是( )
如圖,B,C,E,F四點在一條直線上,AB∥DE,AB=DE,下列條件不能判定△ABC與△DEF全等的是( )| A. | BE=CF | B. | AC=DF | C. | AC∥DF | D. | ∠A=∠D |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 三點確定一個圓 | |
| B. | 平分弦的直徑垂直于弦,并且平分弦所對的兩條弧 | |
| C. | 與直徑垂直的直線是圓的切線 | |
| D. | 能夠互相重合的弧是等弧 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 人數 | 不超過30人 | 超過30人但不超過40人 | 超過40人 |
| 人均旅游費 | 1000元 | 每增加1人,人均旅游費降低20元 | 800元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com