
分析 方法一、由(a,b,c)和$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$均為三角形數,得出a+b>c和$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,聯立兩式,即可得$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}<\frac{{3+\sqrt{5}}}{2}$,再由a≤b≤c,得出$\frac{a}{c}≤1$,即可得出結論;
方法二、設$\frac{a}{c}=k$,同方法一即可得出結論.
解答 解:方法一、∵(a,b,c)為三角形數,
∴a+b>c.
∴b>c-a,
∴$\frac{1}{b}<\frac{1}{c-a}$,
∵$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$為三角形數,
∴$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,
∴$\frac{1}{a}<\frac{1}{b}+\frac{1}{c}<\frac{1}{c-a}+\frac{1}{c}$,
∴$\frac{1}{a}<\frac{1}{c-a}+\frac{1}{c}$,
兩邊同時乘以a(a>0),得,$1<\frac{a}{c-a}+\frac{a}{c}$,
即$\frac{c-a}{c}<\frac{a}{c-a}$,
化簡得,a2-3ac+c2<0,
兩邊除以c2得,${({\frac{a}{c}})^2}-3(\frac{a}{c})+1<0$,
∴$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}<\frac{{3+\sqrt{5}}}{2}$
∵a≤b≤c,
∴$\frac{a}{c}≤1$,
∴$\frac{{3-\sqrt{5}}}{2}<\frac{a}{c}≤1$;
故答案為:$\frac{3-\sqrt{5}}{2}<\frac{c}{a}≤1$.
方法二、設$\frac{a}{c}=k$,
∵(a,b,c)為三角形數,
∴a+b>c,
∴b>c-a,
∴b>(1-k)c,
∴$\frac{1}{b}<\frac{1}{(1-k)c}$,
∵$(\frac{1}{a},\frac{1}{b},\frac{1}{c})$為三角形數,
∴$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$,
∴$\frac{1}{a}<\frac{1}{b}+\frac{1}{c}<\frac{1}{(1-k)c}+\frac{1}{c}$,
∴$\frac{1}{a}<\frac{1}{(1-k)c}+\frac{1}{c}$,
化簡得,k2-3k+1<0,
解得$\frac{{3-\sqrt{5}}}{2}<k<\frac{{3+\sqrt{5}}}{2}$,
∵a≤b≤c,
∴k≤1,
∴$\frac{{3-\sqrt{5}}}{2}<k≤1$,
故答案為:$\frac{3-\sqrt{5}}{2}<\frac{c}{a}≤1$.
點評 此題是三角形邊角關系,主要考查了新定義,三角形的兩邊之和第三邊,解本題的關鍵是列出a+b>c和$\frac{1}{b}+\frac{1}{c}>\frac{1}{a}$兩個不等式,對這兩個式子的化簡是解本題的難點.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
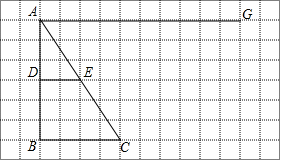 如圖,在網格圖中,有△ABC與線段DE,在線段AG上是否存在點M,使得△MEC與△ADE相似?若存在,請先在圖中確定出所有的點M,并選擇其中一個說明理由;若不存在,也請說明理由.(圖中各點均在格點上).
如圖,在網格圖中,有△ABC與線段DE,在線段AG上是否存在點M,使得△MEC與△ADE相似?若存在,請先在圖中確定出所有的點M,并選擇其中一個說明理由;若不存在,也請說明理由.(圖中各點均在格點上).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
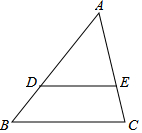 如圖,畫線段DE平行于BC,端點D,E分別在AB,AC上,再畫線段FG平行于CA,HI平行于AB,端點也都分別在另兩邊上,在按上述要求畫出的圖形中,最少有5個三角形,最多有8個三角形.
如圖,畫線段DE平行于BC,端點D,E分別在AB,AC上,再畫線段FG平行于CA,HI平行于AB,端點也都分別在另兩邊上,在按上述要求畫出的圖形中,最少有5個三角形,最多有8個三角形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | m | -3 | … |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 一個長方體盒子的長、寬、高分別為3cm,3cm,5cm,一只螞蟻從盒底的點A沿盒的表面爬到盒頂的點B,螞蟻爬行的最短路程是( )
一個長方體盒子的長、寬、高分別為3cm,3cm,5cm,一只螞蟻從盒底的點A沿盒的表面爬到盒頂的點B,螞蟻爬行的最短路程是( )| A. | $\sqrt{73}$cm | B. | 3$\sqrt{6}$cm | C. | $\sqrt{61}$cm | D. | $\sqrt{53}$cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com