
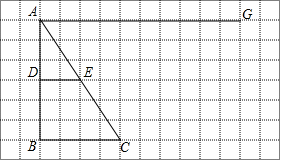
 如圖,在網格圖中,有△ABC與線段DE,在線段AG上是否存在點M,使得△MEC與△ADE相似?若存在,請先在圖中確定出所有的點M,并選擇其中一個說明理由;若不存在,也請說明理由.(圖中各點均在格點上).
如圖,在網格圖中,有△ABC與線段DE,在線段AG上是否存在點M,使得△MEC與△ADE相似?若存在,請先在圖中確定出所有的點M,并選擇其中一個說明理由;若不存在,也請說明理由.(圖中各點均在格點上). 分析 △ADE中,∠ADE=90°,DE是△ABC的中位線,則DE∥BC;如果過點E作EM⊥AC于M,則△AEM中有兩個角與△ADE中的兩個角分別對應相等,根據相似三角形的判定,可知兩三角形相似.
解答 解:存在.
理由:過點E作AC的垂線,與AG交于一點M,點M即為所求.連接MC;
∵AD=DB,AE=EC,
∴DE是△ABC的中位線,
∴DE∥BC,AE=EC.
∵ME⊥AC,
∴△AEM≌△CEM.
∴∠MAE=∠MCE.
∵∠B=90°,
∴∠DAM=90°.
∵AF∥BC,
∴AM∥DE.
∴∠MAE=∠AED.
∴∠AED=∠MCE.
∵∠ADE=∠MEC=90°,
∴△MEC∽△ADE.
點評 本題主要考查相似三角形的判定、全等三角形的判定和性質、三角形的中位線定理等知識,解題的關鍵是學會添加輔助線,構造相似三角形解決問題,綜合性較強,難度適中.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
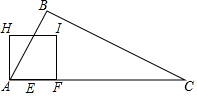 如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動點E從點A出發,以2cm/s的速度沿AC向點C運動;同時動點F從點A出發,以4cm/s的速度沿A-C-A運動;當點E到達終點C時,點F隨之停止運動.作點F關于點E的對稱點G,將線段GF繞點G逆時針旋轉90°得到線段GH,以GF,GH為邊作正方形FGHI,設點E的運動時間為ts.
如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動點E從點A出發,以2cm/s的速度沿AC向點C運動;同時動點F從點A出發,以4cm/s的速度沿A-C-A運動;當點E到達終點C時,點F隨之停止運動.作點F關于點E的對稱點G,將線段GF繞點G逆時針旋轉90°得到線段GH,以GF,GH為邊作正方形FGHI,設點E的運動時間為ts.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 5.88×105 | B. | 5.88×104 | C. | 58.8×103 | D. | 0.588×105 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,則△ABC的面積為42.
如圖,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,則△ABC的面積為42.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com