
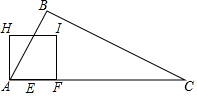
 如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動(dòng)點(diǎn)E從點(diǎn)A出發(fā),以2cm/s的速度沿AC向點(diǎn)C運(yùn)動(dòng);同時(shí)動(dòng)點(diǎn)F從點(diǎn)A出發(fā),以4cm/s的速度沿A-C-A運(yùn)動(dòng);當(dāng)點(diǎn)E到達(dá)終點(diǎn)C時(shí),點(diǎn)F隨之停止運(yùn)動(dòng).作點(diǎn)F關(guān)于點(diǎn)E的對(duì)稱點(diǎn)G,將線段GF繞點(diǎn)G逆時(shí)針旋轉(zhuǎn)90°得到線段GH,以GF,GH為邊作正方形FGHI,設(shè)點(diǎn)E的運(yùn)動(dòng)時(shí)間為ts.
如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動(dòng)點(diǎn)E從點(diǎn)A出發(fā),以2cm/s的速度沿AC向點(diǎn)C運(yùn)動(dòng);同時(shí)動(dòng)點(diǎn)F從點(diǎn)A出發(fā),以4cm/s的速度沿A-C-A運(yùn)動(dòng);當(dāng)點(diǎn)E到達(dá)終點(diǎn)C時(shí),點(diǎn)F隨之停止運(yùn)動(dòng).作點(diǎn)F關(guān)于點(diǎn)E的對(duì)稱點(diǎn)G,將線段GF繞點(diǎn)G逆時(shí)針旋轉(zhuǎn)90°得到線段GH,以GF,GH為邊作正方形FGHI,設(shè)點(diǎn)E的運(yùn)動(dòng)時(shí)間為ts.分析 (1)分兩種情況分別表示FC的長(zhǎng)即可;
(2)當(dāng)F從C到A時(shí),才會(huì)有E與F重合,即當(dāng)2.5<t≤5時(shí),如圖1,點(diǎn)E與點(diǎn)F重合,根據(jù)EC=FC列式解出即可;
(3)由圖形可知:當(dāng)點(diǎn)E與點(diǎn)F重合之后,所成的正方形FGHI在AC的下方,與Rt△ABC無(wú)重疊部分,因此在0≤t≤$\frac{10}{3}$時(shí),當(dāng)正方形FGHI與Rt△ABC重疊部分的圖形是四邊形時(shí),分四種情況討論:
①先計(jì)算當(dāng)I在BC上時(shí)t的值,如圖2,此時(shí)t=$\frac{5}{6}$,
當(dāng)0≤t≤$\frac{5}{6}$時(shí),如圖4,正方形FGHI與Rt△ABC重疊部分的圖形是四邊形AFIG,利用S正方形AFIH-S△AGH可以求得S的關(guān)系式;
②計(jì)算當(dāng)B在HI上時(shí),如圖3,此時(shí)t=1,
當(dāng)1≤t<5時(shí),如圖5,重疊部分的圖形是四邊形AFGB,根據(jù)S=S△ABC-S△CFG可以求得S的關(guān)系式;
③如圖6,點(diǎn)F從C到A時(shí),計(jì)算GH過(guò)點(diǎn)B時(shí),根據(jù)EG=FE,列式計(jì)算t=$\frac{11}{4}$,如圖7,H在BC上時(shí),根據(jù)2GH=GC,計(jì)算t=$\frac{25}{8}$,
當(dāng)$\frac{11}{4}$≤t≤$\frac{25}{8}$時(shí),如圖8,重疊部分的四邊形為GFIH,根據(jù)梯形面積公式求得S的關(guān)系式;
④先計(jì)算當(dāng)I在BC上時(shí),t=$\frac{45}{14}$,
當(dāng)$\frac{45}{14}$≤t≤$\frac{10}{3}$時(shí),重疊部分的四邊形是正方形GFIH,代入面積公式計(jì)算即可;
(4)當(dāng)BI⊥AC時(shí),如圖10,此時(shí)BF⊥AC,利用勾股定理理求AM=2$\sqrt{5}$t,證明△BMI∽△BAF,得AM=$\frac{1}{2}$AB,列式可求得t的值.
解答 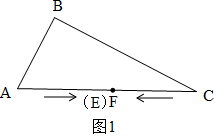 解:(1)當(dāng)0≤t≤2.5時(shí),F(xiàn)C=10-4t;
解:(1)當(dāng)0≤t≤2.5時(shí),F(xiàn)C=10-4t;
當(dāng)2.5<t≤5時(shí),AC+FC=4t,F(xiàn)C=4t-10;
(2)當(dāng)2.5<t≤5時(shí),如圖1,點(diǎn)E與點(diǎn)F重合,
EC=FC,
則10-2t=4t-10,
6t=20,
t=$\frac{10}{3}$,
答:點(diǎn)E與點(diǎn)F重合時(shí)t的值是$\frac{10}{3}$s;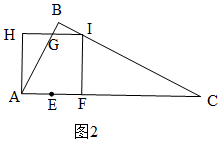
(3)分四種情況:
①當(dāng)I在BC上時(shí),如圖2,
Rt△IFC中,tan∠C=$\frac{FI}{FC}=\frac{1}{2}$,
∴FC=2FI,
10-4t=2×4t,
t=$\frac{5}{6}$,
在Rt△ABC中,設(shè)AB=x,則BC=2x,
由勾股定理得:AC=$\sqrt{5}$x=10,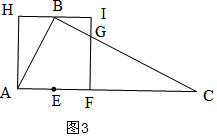
x=2$\sqrt{5}$,
∴AB=2$\sqrt{5}$,BC=4$\sqrt{5}$,
當(dāng)B在HI上時(shí),如圖3,
S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•AH,
2$\sqrt{5}$×$4\sqrt{5}$=10AH,
AH=4,
AH=AF=4t=4,
t=1,
當(dāng)0≤t≤$\frac{5}{6}$時(shí),如圖4,正方形FGHI與Rt△ABC重疊部分的圖形是四邊形AFIG,
∵四邊形AFIH是正方形,
∴∠HAF=90°,AF=AH=4t,
∴∠HAG+∠GAF=90°,
∵∠B=90°,
∴∠C+∠GAF=90°,
∴∠C=∠HAG,
∵AB=$\frac{1}{2}$BC,
∴tan∠C=tan∠HAG=$\frac{AB}{BC}=\frac{1}{2}$,
∴$\frac{GH}{AH}$=$\frac{1}{2}$,
∴AH=2GH=4t,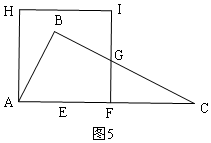
∴GH=2t,
∴S=S正方形AFIH-S△AGH=4t•4t-$\frac{1}{2}$•2t•4t=12t2;
②當(dāng)1≤t<5時(shí),如圖5,重疊部分的圖形是四邊形AFGB,
∵FC=10-4t,
∴FG=$\frac{1}{2}$FC=5-2t,
∴S=S△ABC-S△CFG=$\frac{1}{2}$×$2\sqrt{5}$×$4\sqrt{5}$-$\frac{1}{2}$(5-2t)(10-4t),
S=-4t2+20t-5,
③如圖6,點(diǎn)F從C到A時(shí),當(dāng)GH過(guò)點(diǎn)B,
在Rt△ABG中,cos∠A=$\frac{AG}{AB}=\frac{AB}{AC}$,
∴$\frac{AG}{2\sqrt{5}}=\frac{2\sqrt{5}}{10}$,
∴AG=2,
∵FC=4t-10,
由G與F關(guān)于點(diǎn)E對(duì)稱得:EG=FE,
AE-AG=EC-FC,
2t-2=10-2t-(4t-10),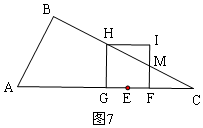
t=$\frac{11}{4}$,
如圖7,H在BC上時(shí),
∵EF=EC-FC=10-2t-(4t-10)=20-6t,
∴GH=2EF=2(20-6t)=40-12t,
tan∠C=$\frac{GH}{GC}=\frac{1}{2}$,
∴2GH=GC,
2(40-12t)=40-12t+4t-10,
40-12t=4t-10,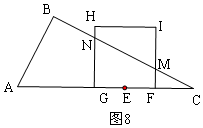
16t=50,
t=$\frac{25}{8}$,
當(dāng)$\frac{11}{4}$≤t≤$\frac{25}{8}$時(shí),如圖8,重疊部分的四邊形為GFMN,
FM=$\frac{1}{2}$FC=2t-5,
GC=2EF+FC=40-12t+4t-10=30-8t,
GN=$\frac{1}{2}$GC=15-4t,
∴S=S梯形GFMN=$\frac{1}{2}$(FM+GN)•GF=$\frac{1}{2}$(2t-5+15-4t)(40-12t),
S=12t2-100t+300,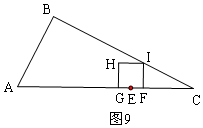
④如圖9,當(dāng)I在BC上時(shí),
FI=$\frac{1}{2}$CF=2t-5,
FG=40-12t,
∵FG=FI,
∴40-12t=2t-5,
t=$\frac{45}{14}$,
當(dāng)$\frac{45}{14}$≤t≤$\frac{10}{3}$時(shí),重疊部分的四邊形是正方形GFIH,
S=GF2=(40-12t)2=144t2-960t+1600,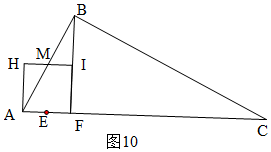
綜上所述,重疊部分圖形的面積S與t的函數(shù)關(guān)系式:S=$\left\{\begin{array}{l}{12{t}^{2}(0≤t≤\frac{5}{6})}\\{-4{t}^{2}+20t-5(1≤t<5)}\\{12{t}^{2}-100t+300(\frac{11}{4}≤t≤\frac{25}{8})}\\{144{t}^{2}-960t+1600(\frac{45}{14}≤t≤\frac{10}{3})}\end{array}\right.$;
(4)當(dāng)BI⊥AC時(shí),如圖10,此時(shí)BF⊥AC,
在Rt△AHM中,AH=4t,HM=2t,
由勾股定理理:AM=$\sqrt{(4t)^{2}+(2t)^{2}}$=2$\sqrt{5}$t,
∴MI=HI-HM=4t-2t=2t,
∵M(jìn)I∥AF,
∴△BMI∽△BAF,
∴$\frac{BM}{AB}=\frac{MI}{AF}$=$\frac{2t}{4t}$=$\frac{1}{2}$,
∴AB=2BM,
∴AM=$\frac{1}{2}$AB,
2$\sqrt{5}$t=$\frac{1}{2}$×$2\sqrt{5}$,
t=$\frac{1}{2}$,
則直線BI與AC垂直時(shí)t的值是$\frac{1}{2}$.
點(diǎn)評(píng) 本題是四邊形的綜合題,難度較大,容易丟解,尤其是第三問(wèn);還考查了正方形的性質(zhì)、勾股定理、動(dòng)點(diǎn)運(yùn)動(dòng)的問(wèn)題、同角的三角函數(shù)以及三角形相似的性質(zhì)和判定,并與二次函數(shù)相結(jié)合,根據(jù)多邊形的面積公式或和差的關(guān)系求解二次函數(shù)的關(guān)系式,注意第三問(wèn)中重疊部分是四邊形時(shí)的t的取值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
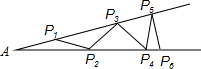 課本“目標(biāo)與評(píng)定”中有這樣一道思考題,如圖鋼架中,∠A=20°,焊上等長(zhǎng)的鋼條來(lái)加固鋼架,若AP1=P1P2,問(wèn)這樣的鋼條至多需要多少根?
課本“目標(biāo)與評(píng)定”中有這樣一道思考題,如圖鋼架中,∠A=20°,焊上等長(zhǎng)的鋼條來(lái)加固鋼架,若AP1=P1P2,問(wèn)這樣的鋼條至多需要多少根?查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
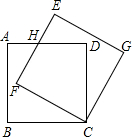 如圖,邊長(zhǎng)為10的正方形ABCD繞點(diǎn)C按順時(shí)針?lè)较蛐D(zhuǎn)30°后得到正方形EFCG,EF交AD于點(diǎn)H,那么DH的長(zhǎng)為$\frac{10\sqrt{3}}{3}$.
如圖,邊長(zhǎng)為10的正方形ABCD繞點(diǎn)C按順時(shí)針?lè)较蛐D(zhuǎn)30°后得到正方形EFCG,EF交AD于點(diǎn)H,那么DH的長(zhǎng)為$\frac{10\sqrt{3}}{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
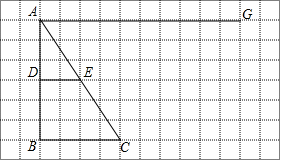 如圖,在網(wǎng)格圖中,有△ABC與線段DE,在線段AG上是否存在點(diǎn)M,使得△MEC與△ADE相似?若存在,請(qǐng)先在圖中確定出所有的點(diǎn)M,并選擇其中一個(gè)說(shuō)明理由;若不存在,也請(qǐng)說(shuō)明理由.(圖中各點(diǎn)均在格點(diǎn)上).
如圖,在網(wǎng)格圖中,有△ABC與線段DE,在線段AG上是否存在點(diǎn)M,使得△MEC與△ADE相似?若存在,請(qǐng)先在圖中確定出所有的點(diǎn)M,并選擇其中一個(gè)說(shuō)明理由;若不存在,也請(qǐng)說(shuō)明理由.(圖中各點(diǎn)均在格點(diǎn)上).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com