
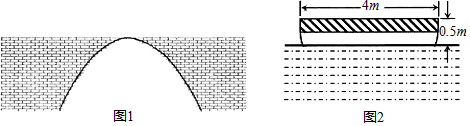
分析 (1)建立適當的坐標系,由待定系數法求出函數解析式,即可得出結果;
(2)利用已知得出x=2時,y的值,進而得出答案.
解答 解:(1)如圖所示: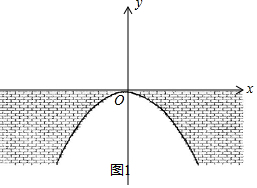
設函數解析式為y=ax2,B(3,-3),A(-3,-3),
把點B坐標代入得:9a=-3,
解得:a=-$\frac{1}{3}$,
即y=-$\frac{1}{3}$x2,
當y=-2時,-$\frac{1}{3}$x2=-2,
解得:x=±$\sqrt{6}$,
故此時水面寬度為2$\sqrt{6}$.
(2)當x=2時,y=-$\frac{4}{3}$,
因為船上貨物最高點距拱頂1.5米,且|-$\frac{4}{3}$|<1.5,所以這艘船能從橋下通過.
點評 此題主要考查了二次函數的應用以及圖象上點的坐標性質;建立適當的坐標系,根據題意確定點的坐標求出函數解析式是解題關鍵.


 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖三角形中,請完成下列操作:
已知:如圖三角形中,請完成下列操作:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
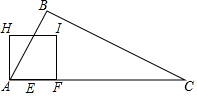 如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動點E從點A出發,以2cm/s的速度沿AC向點C運動;同時動點F從點A出發,以4cm/s的速度沿A-C-A運動;當點E到達終點C時,點F隨之停止運動.作點F關于點E的對稱點G,將線段GF繞點G逆時針旋轉90°得到線段GH,以GF,GH為邊作正方形FGHI,設點E的運動時間為ts.
如圖,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,動點E從點A出發,以2cm/s的速度沿AC向點C運動;同時動點F從點A出發,以4cm/s的速度沿A-C-A運動;當點E到達終點C時,點F隨之停止運動.作點F關于點E的對稱點G,將線段GF繞點G逆時針旋轉90°得到線段GH,以GF,GH為邊作正方形FGHI,設點E的運動時間為ts.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,則△ABC的面積為42.
如圖,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,則△ABC的面積為42.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com