
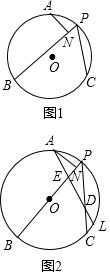
 在⊙O中,PB、PC為⊙O的弦,點A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,過點A作AN⊥PB于點N,
在⊙O中,PB、PC為⊙O的弦,點A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,過點A作AN⊥PB于點N,分析 (1)作輔助線,構建全等三角形,證明△ABN≌△ACG和Rt△ANP≌Rt△AGP,再利用線段的和可以得出結論;
(2)如圖2,連接AP、BC、OA,過D作DH⊥PB于H,根據(1)的結論證明直徑BP=10,利用勾股定理求BC=6,證明△ANE≌△DHE,則AN=DH=3,EH=EN,再證明△DHP∽△BCP求PH=4,PD=5,則CD=3,利用勾股定理求AE的長,則可得AD的長,利用△ADP∽△CDL,得DL=$\sqrt{5}$.
解答 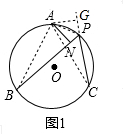 證明:(1)如圖1,連接AB、AC、AP,過A作AG⊥PC,交CP的延長線于G,
證明:(1)如圖1,連接AB、AC、AP,過A作AG⊥PC,交CP的延長線于G,
∴∠AGC=90°,
∵AN⊥BP,
∴∠ANB=90°,
∴∠AGC=∠ANB,
∵$\widehat{AB}$=$\widehat{AC}$,
∴AB=AC,
在△ABN和△ACG中,
∵$\left\{\begin{array}{l}{∠ANB=∠AGC}\\{∠B=∠C}\\{AB=AC}\end{array}\right.$,
∴△ABN≌△ACG(AAS),
∴BN=CG,AN=AG,
在Rt△ANP和Rt△AGP中,
∵$\left\{\begin{array}{l}{AN=AG}\\{AP=AP}\end{array}\right.$,
∴Rt△ANP≌Rt△AGP(HL),
∴PN=PG,
∴BN=CG=PG+PC=PN+PC;
(2)如圖2,連接AP、BC、OA,過D作DH⊥PB于H,
由(1)得:BN=PN+PC=1+8=9,
∴PB=BN+PN=9+1=10,
∴OA=OP=5,ON=OP-PN=5-1=4,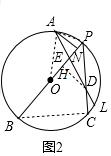
在Rt△AON中,AN=3,
∵PB是⊙O的直徑,
∴∠BCP=90°,
由勾股定理得:BC=6,
在△ANE和△DHE中,
∵$\left\{\begin{array}{l}{∠ANE=∠DHE=90°}\\{∠AEN=∠DEH}\\{AE=DE}\end{array}\right.$,
∴△ANE≌△DHE(AAS),
∴AN=DH=3,EH=EN,
∵∠DHP=∠BCP=90°,
∠BPC=∠HPD,
∴△DHP∽△BCP,
∴$\frac{DH}{BC}=\frac{PH}{PC}=\frac{PD}{BP}$,
∴$\frac{3}{6}=\frac{PH}{8}=\frac{PD}{10}$,
∴PH=4,PD=5,
∴DC=PC-PD=8-5=3,
HN=PH-PN=4-1=3,
∴EN=$\frac{1}{2}$HN=$\frac{3}{2}$,
在Rt△AEN中,AE=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
∴AD=2AE=3$\sqrt{5}$,
∵∠DAP=∠DCL,∠ADP=∠CDL,
∴△ADP∽△CDL,
∴$\frac{AD}{CD}=\frac{PD}{DL}$,
∴$\frac{3\sqrt{5}}{3}=\frac{5}{DL}$,
∴DL=$\sqrt{5}$.
點評 本題考查了相似、全等三角形的性質和判定、圓周角定理等知識,作輔助線構建全等三角形是關鍵,明確直徑所對的圓周角是直角,利用相似和全等三角形邊的關系求線段的長,從而使問題得以解決.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
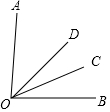 如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.
如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2 | B. | 1 | C. | 2017 | D. | 2016 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 方程沒有實數根 | |
| B. | 方程有兩個不相等的正實數根或有兩個不相等的負實數根 | |
| C. | 方程有一個正實數根和一個負實數根,且正實數根的絕對值較大 | |
| D. | 方程有一個正實數根和一個負實數根,且負實數根的絕對值較大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com