
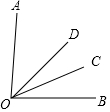
 如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.
如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.分析 (1)根據角平分線的定義得到∠DOB=$\frac{1}{2}$∠AOB,根據已知得到∠BOC=$\frac{1}{4}$∠AOB,根據等量關系得到∠COD=$\frac{1}{4}$∠AOB,可得∠BOC=∠COD,再根據角平分線的定義即可求解;
(2)由(1)得到∠AOB=4∠COD,再代值計算即可求解.
解答 解:(1)OC是∠DOB的平分線,理由如下:
∵OD是∠AOB的平分線,
∴∠DOB=$\frac{1}{2}$∠AOB,
∵∠AOC=3∠BOC,
∴∠BOC=$\frac{1}{4}$∠AOB,
∴∠COD=∠DOB-∠BOC=$\frac{1}{2}$∠AOB-$\frac{1}{4}$∠AOB=$\frac{1}{4}$∠AOB,
∴∠BOC=∠COD,
∴OC是∠DOB的平分線;
(2)∵∠COD=$\frac{1}{4}$∠AOB,
∴∠AOB=4∠COD=84°.
點評 本題主要考查了角度的計算,角平分線的定義,分別用∠AOB表示出∠BOC與∠COD是解題的關鍵.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
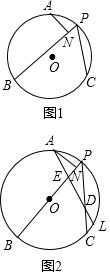 在⊙O中,PB、PC為⊙O的弦,點A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,過點A作AN⊥PB于點N,
在⊙O中,PB、PC為⊙O的弦,點A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,過點A作AN⊥PB于點N,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
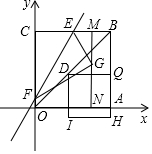 如圖,四邊形OABC是一張放在平面直角坐標中的正方形紙片,點O與坐標原點重合,點A 在x軸上,點C在y軸上,OC=4,點E為BC的中點,點N的坐標為(3,0),過點 N且平行于y軸的直線MN與EB交于點M.現將紙片折疊,使頂點C落在MN上,并與MN上的點G重合,折痕為EF,點F為折痕與y軸的交點.連接OB,D為OB上動點,作DQ∥x軸交BA于點Q,以DQ為邊,向下作正方形DQHI,設點D的橫坐標為t.
如圖,四邊形OABC是一張放在平面直角坐標中的正方形紙片,點O與坐標原點重合,點A 在x軸上,點C在y軸上,OC=4,點E為BC的中點,點N的坐標為(3,0),過點 N且平行于y軸的直線MN與EB交于點M.現將紙片折疊,使頂點C落在MN上,并與MN上的點G重合,折痕為EF,點F為折痕與y軸的交點.連接OB,D為OB上動點,作DQ∥x軸交BA于點Q,以DQ為邊,向下作正方形DQHI,設點D的橫坐標為t.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
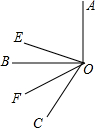 已知:如圖∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
已知:如圖∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正確的是( )
如圖,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正確的是( )| A. | sinA=$\frac{BD}{BC}$ | B. | cosA=$\frac{AC}{AD}$ | C. | tanA=$\frac{CD}{AB}$ | D. | cosB=$\frac{AC}{AB}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
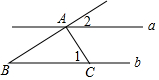 如圖,已知直線a∥b,AC⊥AB,AC與直線a,b分別交于A,C兩點,若∠1=60°,則∠2的度數為( )
如圖,已知直線a∥b,AC⊥AB,AC與直線a,b分別交于A,C兩點,若∠1=60°,則∠2的度數為( )| A. | 30° | B. | 35° | C. | 45° | D. | 50° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com