
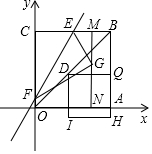
 如圖,四邊形OABC是一張放在平面直角坐標(biāo)中的正方形紙片,點(diǎn)O與坐標(biāo)原點(diǎn)重合,點(diǎn)A 在x軸上,點(diǎn)C在y軸上,OC=4,點(diǎn)E為BC的中點(diǎn),點(diǎn)N的坐標(biāo)為(3,0),過點(diǎn) N且平行于y軸的直線MN與EB交于點(diǎn)M.現(xiàn)將紙片折疊,使頂點(diǎn)C落在MN上,并與MN上的點(diǎn)G重合,折痕為EF,點(diǎn)F為折痕與y軸的交點(diǎn).連接OB,D為OB上動(dòng)點(diǎn),作DQ∥x軸交BA于點(diǎn)Q,以DQ為邊,向下作正方形DQHI,設(shè)點(diǎn)D的橫坐標(biāo)為t.
如圖,四邊形OABC是一張放在平面直角坐標(biāo)中的正方形紙片,點(diǎn)O與坐標(biāo)原點(diǎn)重合,點(diǎn)A 在x軸上,點(diǎn)C在y軸上,OC=4,點(diǎn)E為BC的中點(diǎn),點(diǎn)N的坐標(biāo)為(3,0),過點(diǎn) N且平行于y軸的直線MN與EB交于點(diǎn)M.現(xiàn)將紙片折疊,使頂點(diǎn)C落在MN上,并與MN上的點(diǎn)G重合,折痕為EF,點(diǎn)F為折痕與y軸的交點(diǎn).連接OB,D為OB上動(dòng)點(diǎn),作DQ∥x軸交BA于點(diǎn)Q,以DQ為邊,向下作正方形DQHI,設(shè)點(diǎn)D的橫坐標(biāo)為t.分析 (1)在Rt△EMG中,根據(jù)EM=1,EC=EG=2,推出∠EGM=30°,由此即可求出MG,求出點(diǎn)G坐標(biāo),再在Rt△CFE中,證明∠CFE=30°,即可求出點(diǎn)F坐標(biāo),利用待定系數(shù)法即可解決問題.
(2)分兩種情形①如圖1中,當(dāng)0<t≤2時(shí),重疊部分是四邊形DQAK.②如圖2中,當(dāng)2<t<4時(shí),重疊部分是正方形DQHI.分別求解即可.
(3)如圖3中,分四種情形求解即可解決問題.
解答 解:(1)∵四邊形ABCO是正方形,
∴BC=OA=4,
∵E為CB中點(diǎn),
∴EB=2,
∵M(jìn)N∥y軸,N(3,0),
∴MN⊥EB且MB=NA=1,
∴EM=1,
而EG=EC=2,
∴sin∠EGM=$\frac{EM}{EG}$=$\frac{1}{2}$,
∴∠EGM=30°,
∴MG=EGcos30°=$\sqrt{3}$,
∴G(3,4-$\sqrt{3}$);
∵∠EGM=30°,
∴∠MEG=∠FEG=∠CEF=60°,
∴CF=CEtan60°=2 $\sqrt{3}$,
∴FO=4-2 $\sqrt{3}$,
∴F(0,4-2 $\sqrt{3}$),E(2,4),
設(shè)直線EF的解析式:y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{2k+b=4}\\{b=4-2\sqrt{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=4-2\sqrt{3}}\end{array}\right.$,
∴折痕EF所在直線解析式:y=$\sqrt{3}$x+4-2 $\sqrt{3}$;
(2)①如圖1中,當(dāng)0<t≤2時(shí),重疊部分是四邊形DQAK.
S=DK•AK=t(4-t)=-t2+4t.
②如圖2中,當(dāng)2<t<4時(shí),重疊部分是正方形DQHI.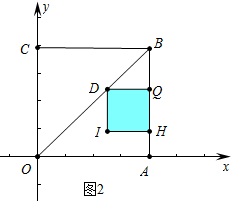
S=DQ2=(4-t)2,
綜上所述S=$\left\{\begin{array}{l}{-{t}^{2}+4t}&{(0<t≤2)}\\{(4-t)^{2}}&{(2<t<4)}\end{array}\right.$.
(3)如圖3中,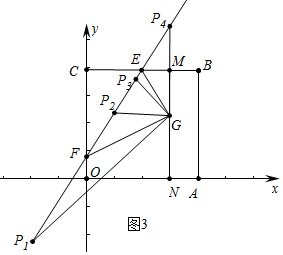
當(dāng)FG=FP1時(shí),∵FG=FC=2$\sqrt{3}$,∠OFP1=30°,可得P1(-$\sqrt{3}$,1-2$\sqrt{3}$),
當(dāng)P2F=P2G時(shí),∵∠P2FG=∠P2GF=30°,△P2EG是等邊三角形,可得P2(1,4-$\sqrt{3}$),
當(dāng)FG=FP3時(shí),∵FG=FP3=2$\sqrt{3}$,∠GFP3=30°,可得P3($\sqrt{3}$,7-2$\sqrt{3}$),
當(dāng)GF=GP4時(shí),G、M、P4共線,易知P4(3,4+$\sqrt{3}$),
綜上所述,滿足條件的點(diǎn)P坐標(biāo)為(-$\sqrt{3}$,1-2 $\sqrt{3}$)或(1,4-$\sqrt{3}$)或( $\sqrt{3}$,7-2 $\sqrt{3}$)或(3,4+$\sqrt{3}$).
點(diǎn)評(píng) 本題考查四邊形綜合運(yùn)用、正方形的性質(zhì)、矩形的性質(zhì)、等腰三角形的性質(zhì)和判定、勾股定理,直角三角形30度角性質(zhì)、銳角三角函數(shù)等知識(shí),解題的關(guān)鍵是會(huì)靈活的運(yùn)用所學(xué)知識(shí)解決問題,學(xué)會(huì)用分類討論的思想思考問題,屬于中考?jí)狠S題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖:點(diǎn)P是線段AB上任意一點(diǎn),且C、D分別為線段AP、BP的中點(diǎn),若CD=5cm,則有AB=10cm.
如圖:點(diǎn)P是線段AB上任意一點(diǎn),且C、D分別為線段AP、BP的中點(diǎn),若CD=5cm,則有AB=10cm.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{7}$ | C. | $\sqrt{24}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,△ABC的頂點(diǎn)都是正方形網(wǎng)格中的格點(diǎn),則tan∠ABC=$\frac{1}{2}$.
如圖,△ABC的頂點(diǎn)都是正方形網(wǎng)格中的格點(diǎn),則tan∠ABC=$\frac{1}{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.296868×104 | B. | 2.96868×105 | C. | 2.96868×106 | D. | 29.6868×104 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
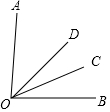 如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.
如圖,OD是∠AOB的平分線,∠AOC=3∠BOC,∠COD=21°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
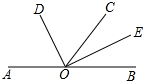 填空,完成下列說理過程:
填空,完成下列說理過程:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個(gè) | B. | 3個(gè) | C. | 4個(gè) | D. | 5個(gè) |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com