
分析 利用拋物線的圖象性質(zhì)可以知道拋物線y=x2的圖象開口向上最低點為原點,它與直線有交點則可以聯(lián)立求解方程有兩個實數(shù)根,便可一切定出t的取值范圍.
解答 解:聯(lián)立y=x2與y=tx-c,
消去y得二次方程x2-tx+c=0①
有實數(shù)根x1,x2,則x1+x2=t,x1x2=c.
所以c=x1x2=$\frac{1}{2}$[(x1+x2)2-(x12+x22)]=$\frac{1}{2}$[t2-(t2-2t-3)]=t+$\frac{3}{2}$②
把②式代入方程①得x2-tx+t+$\frac{3}{2}$=0③
t的取值應(yīng)滿足t2-2t-3=x12+x22≥0,④
且使方程③有實數(shù)根,即△=t2-4(t+$\frac{3}{2}$)=t2-4t-6≥0,⑤
解不等式④得t≤-1或t≥3,
解不等式⑤得t≥2+$\sqrt{10}$或t≤2-$\sqrt{10}$.
所以,t的取值范圍為t≤2-$\sqrt{10}$或t≥2+$\sqrt{10}$.
點評 本題考查了二次函數(shù)的圖象性質(zhì),以及二次函數(shù)求最值的相關(guān)知識,難度較大.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.5米 | B. | 1米 | C. | 1.5米 | D. | 2米 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知實數(shù)a,b,c在數(shù)軸上的位置如圖,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值.
已知實數(shù)a,b,c在數(shù)軸上的位置如圖,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5cm | B. | $\frac{25}{π}$cm | C. | 10cm | D. | 25cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
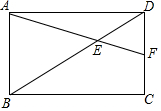 如圖,在矩形ABCD中,AB=6,BC=8,點E在對角線BD上,且BE=6,連接AE并延長交DC于點F,則CF等于( )
如圖,在矩形ABCD中,AB=6,BC=8,點E在對角線BD上,且BE=6,連接AE并延長交DC于點F,則CF等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com