
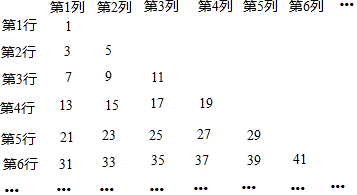
分析 根據(jù)連續(xù)奇數(shù)的排列方式可得出:第n行有n個數(shù),且每個數(shù)均為奇數(shù).
(1)根據(jù)第6行的最后一個數(shù)字,將其+2×7即可得出第7行的最后一個數(shù)字,由第15行第一個數(shù)字為1+(1+2+3+…+14)×2,將其+2×3即可得出第15行第4列數(shù)字;
(2)根據(jù)第1、2、3、…、(n-1)行數(shù)的個數(shù)結合第一行第1個數(shù)字即可得出第n行第1個數(shù)字;再由第n行最后一個數(shù)字為第(n+1)行第一個數(shù)字-2即可得出結論;
(3)根據(jù)(2)找出第50、51行第一個數(shù)字,由此即可找出第50、51行第k、(k+1)列的四個數(shù),將其相加令其=10016即可得出關于k的一元一次方程,解之即可得出結論.
解答 解:觀察發(fā)現(xiàn):第1行1個數(shù),第2行2個數(shù),第3行3個數(shù),第4行4個數(shù),…,
∴第n行有n個數(shù),且每個數(shù)均為奇數(shù).
(1)∵第6行最后一個數(shù)字為41,
∴第7行最后一個數(shù)字為41+2×7=55;
∵第15行第1列數(shù)字為1+(1+2+3+…+14)×2=211,
∴第15行第4列數(shù)字為211+2×3=217.
故答案為:55;217.
(2)第n行的第1個數(shù)字為1+2×[1+2+3+…+(n-1)]=1+n(n-1)=n2-n+1;
第n行的最后一個數(shù)字為1+2×(1+2+3+…+n)-2=1+n(n+1)-2=n2+n-1.
(3)能.理由如下:
∵第50行的第一個數(shù)字為502-50+1=2451,第51行的第一個數(shù)字為512-51+1=2551,
∴第50行第k個數(shù)為2451+2k、第k+1個數(shù)為2451+2(k+1);
第51行第k個數(shù)為2551+2k、第k+1個數(shù)為2551+2(k+1),
∴2451+2k+2451+2(k+1)+2551+2k+2551+2(k+1)=10016,即10008+4k=10016,
解得:k=2,
∴這四個數(shù)分別為:2453,2455,2553,2555.
點評 本題考查了一元一次方程的應用、列代數(shù)式以及規(guī)律型中數(shù)字的變化類,解題的關鍵是:(1)根據(jù)的數(shù)字的分布找出每行中數(shù)字的個數(shù);(2)根據(jù)第n行數(shù)字的個數(shù)為n找出第n行第1個、最后一個數(shù)字;(3)根據(jù)4個數(shù)之和為10016列出關于k的一元一次方程.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數(shù)學 來源: 題型:選擇題
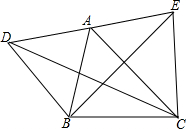 如圖,A為DE的中點,設S1=S△DBC,S2=S△ABC,S3=S△EBC,則S1,S2,S3的關系是( )
如圖,A為DE的中點,設S1=S△DBC,S2=S△ABC,S3=S△EBC,則S1,S2,S3的關系是( )| A. | S2=$\frac{3}{2}$(S1+S3) | B. | S2=$\frac{1}{2}$(S3-S1) | C. | S2=$\frac{1}{2}$(S1+S3) | D. | S2=$\frac{3}{2}$(S3-S1) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 矩形OABC在平面直角坐標系中的位置如圖所示,點B的坐標為(3,4),點D是OA的中點,點E在線段AB上,當△CDE的周長最小時,求點E的坐標.
矩形OABC在平面直角坐標系中的位置如圖所示,點B的坐標為(3,4),點D是OA的中點,點E在線段AB上,當△CDE的周長最小時,求點E的坐標.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,AF是△ABC的高,點D、E分別在AB、AC上,且DE||BC,DE交AF于點G,設AD=5,AB=15,AC=12,GF=6.
如圖,AF是△ABC的高,點D、E分別在AB、AC上,且DE||BC,DE交AF于點G,設AD=5,AB=15,AC=12,GF=6.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| A | B | |
| 進價(萬元/.套) | 1.5 | 1.2 |
| 售價(萬元/套) | 1.65 | 1.4 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com