Question

18．如圖，已知△BAD和△BCE均為等腰直角三角形，∠BAD=∠BCE=90°，點M為DE的中點，過點E與AD平行的直線交射線AM于點N．
（1）當A、B、C三點在同一直線上時（如圖1），求證：M為AN的中點；
（2）將圖1中△BCE繞點B旋轉，當A、B、E三點在同一直線上（如圖2），求證：△CAN為等腰直角三角形；
（3）將圖1中△BCE繞點B旋轉到圖3的位置時，（2）中的結論是否仍然成立？若成立，試證明之；若不成立，請說明理由．

Answer 1

分析 （1）由EN∥AD和點M為DE的中點，可以證得△ADM≌△NEM，從而證得M為AN的中點；
（2）根據已知條件，易證AB=DA=NE，∠ABC=∠NEC=135°，從而可得△ABC≌△NEC，進而可以證得AC=NC，∠ACN=∠BCE=90°，可得△ACN為等腰直角三角形；
（3）根據已知條件，易得△ADM≌△NEM，根據四邊形BCEF內角和為360°，可得∠ABC=∠FEC，從而可以證得△ABC≌△NEC，進而可以證得AC=NC，∠ACN=∠BCE=90°，即可得出△ACN為等腰直角三角形．

解答 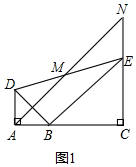解：（1）證明：如圖1，∵EN∥AD，
∴∠MAD=∠MNE，∠ADM=∠NEM，
∵點M為DE的中點，
∴DM=EM，
在△ADM和△NEM中，
$\left\{\begin{array}{l}{∠MAD=∠MNE\\;}\\{∠ADM=∠NEM}\\{DM=EM}\end{array}\right.$，
∴△ADM≌△NEM（AAS），
∴AM=MN，
∴M為AN的中點．

（2）證明：如圖2，∵△BAD和△BCE均為等腰直角三角形，
∴AB=AD，CB=CE，∠CBE=∠CEB=45°，
∵AD∥NE，
∴∠DAE+∠NEA=180°，
∵∠DAE=90°，
∴∠NEA=90°，
∴∠NEC=135°，
∵A，B，E三點在同一直線上，
∴∠ABC=180°-∠CBE=135°，
∴∠ABC=∠NEC，
∵△ADM≌△NEM（已證），
∴AD=NE，
∵AD=AB，
∴AB=NE，
在△ABC和△NEC中，
$\left\{\begin{array}{l}{AB=NE}\\{∠ABC=∠NEC}\\{BC=EC}\end{array}\right.$，
∴△ABC≌△NEC（SAS），
∴AC=NC，∠ACB=∠NCE，
∵∠BCE=90°，
∴∠ACN=∠BCE=90°，
∴△ACN為等腰直角三角形． 

（3）△ACN仍為等腰直角三角形．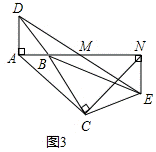
證明：如圖3，A、B、N三點在同一條直線上，
∵AD∥EN，∠DAB=90°，
∴∠ENA=∠DAN=90°，
∵∠BCE=90°，
∴∠CBN+∠CEN=360°-90°-90°=180°，
∵A、B、N三點在同一條直線上，
∴∠ABC+∠CBN=180°，
∴∠ABC=∠NEC，
∵△ADM≌△NEM（已證），
∴AD=NE，
∵AD=AB，
∴AB=NE，
在△ABC和△NEC中，
$\left\{\begin{array}{l}{AB=NE}\\{∠ABC=∠NEC}\\{BC=EC}\end{array}\right.$，
∴△ABC≌△NEC（SAS），
∴AC=NC，∠ACB=∠NCE，
∴∠ACN=∠BCE=90°，
∴△ACN為等腰直角三角形．

點評 本題屬于三角形綜合題，主要考查了全等三角形的判定與性質、平行線的性質、等腰直角三角形的判定與性質、多邊形的內角和等知識的綜合應用，滲透了變中有不變的辯證思想，解決問題的關鍵是掌握等腰直角三角形的判定方法．