Question

8．如圖，直線l的解析式為y=-$\frac{4}{3}$x+b，它與坐標軸分別交于A、B兩點，其中B坐標為（0，4）．
（1）求出A點的坐標；
（2）若點 P在y軸上，且到直線l的距離為3，試求點P的坐標；（ 選做）
（3）在第一象限的角平分線上是否存在點Q使得∠QBA=90°？若存在，求點Q的坐標；若不存在，請說明理由．
（4）動點C從y軸上的點（0，10）出發，以每秒1cm的速度向負半軸運動，求出點C運動所有的時間t，使得△ABC為軸對稱圖形．

Answer 1

分析 （1）利用點B代入直線，求出直線解析式，然后求直線與x軸交點坐標；
（2）已知點到直線距離，可以做點到直線的垂線，構造直角三角形，利用三角形相似就出對應線段長度，繼而求出點的坐標；
（3）點Q在第一象限角平分線上，設Q（x，x），已知給出了指定角，利用勾股定理列方程，即可求出點Q的坐標；
（4）由條件可知△ABC為等腰三角形，可設C點坐標為（0，y），則可用y分別表示出BC、AC，根據等腰三角形性質分AB=BC、AB=AC和BC=AC三種情況，可分別得到關于y的方程，可求得C點坐標，則可求得運動時間．

解答 解：
（1）將點B（0，4）代入直線l的解析式得b=4，
∴直線l的解析式為：y=-$\frac{4}{3}$x+4，
令y=0可得-$\frac{4}{3}$x+4=0，解得x=3，
∴A（3，0）；
（2）如圖，過點P做直線AB的垂線，垂足為D，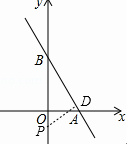

∵OB=4，OA=3，
∴AB=5，
∵∠B是公共角，∠BDP=∠BOD，
∴△BOA∽△BDP，
∴$\frac{OA}{PD}$=$\frac{AB}{BP}$，
∴$\frac{3}{3}$=$\frac{5}{BP}$，
∴BP=5，
∵OB=4，
∴當點P在B點上方進，PB=4+5=9，當點P在B點下方時，PB=4-5=-1，
∴P點坐標為（0，9）或（0，-1）；
（3）存在．理由如下：
∵Q在第一象限的角平分線上，
設Q（x，x），由勾股定理可得QB²+BD²=QD²，
∴x²+（x-4）²+5²=x²+（x-3）²，解得x=16，
∴Q（16，16），
即存在滿足條件的Q點；
（4）設C點坐標為（0，y）（y≤10），則BC=|4-y|，AC=$\sqrt{{3}^{2}+{y}^{2}}$=$\sqrt{{y}^{2}+9}$，且AB=5，
當△ABC為軸對稱圖形，則△ABC為等腰三角形，
∴有AB=BC、AB=AC和BC=AC三種情況
①當AB=BC時，即|4-y|=5，解得y=9或y=-1，
∴C（0，9）或（0，-1），
∴t=10-9=1或t=10-（-1）=11，
即此時C點運動時間為1秒或11秒；
②當AB=AC時，即$\sqrt{{y}^{2}+9}$=5，解得y=4或y=-4，
∴C（0，4）或（0，-4），但當點C在x軸上方時不合題意，舍去，
∴t=10-（-4）=14，
即此時C點運動時間為14秒；
③當BC=AC時，即BC²=AC²，即|4-y|²=y²+9，解得y=$\frac{7}{8}$，
∴C（0，$\frac{7}{8}$），
∴t=10-$\frac{7}{8}$=$\frac{73}{8}$，
即此時C點運動時間為$\frac{73}{8}$秒；
綜上可知當C點運動1秒、$\frac{73}{8}$秒、11秒或14秒時，使得△ABC為軸對稱圖形．

點評 本題為一次函數的綜合應用，涉及點的坐標、相似三角形判定及性質、勾股定理、軸對稱圖形、等腰三角形的性質、分類討論思想及方程思想等知識點．在（1）中利用B點坐標求得直線解析式即可求得A點坐標，在（2）中求得PB的長是解題的關鍵，在（3）中利用勾股定理得出關于Q點坐標的方程是解題的關鍵，在（3）中化動為靜，求得C點的坐標是解題的關鍵．本題考查知識點較多，綜合性較強，難度適中．