

分析 (1)如圖1中,延長(zhǎng)FH交BC的延長(zhǎng)線于M,由△FDH≌△MCH,推出FH=HM,再利用直角三角形斜邊中線的性質(zhì)即可解決問題.
(2)分兩種情形①當(dāng)FD=FH時(shí),設(shè)∠M=∠DFH=x,構(gòu)建方程解決問題.②當(dāng)∠D=90°時(shí),易知DF=DH,△DEF是等腰直角三角形.
解答 (1)證明:如圖1中,延長(zhǎng)FH交BC的延長(zhǎng)線于M/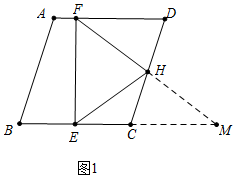
∵四邊形ABCD是菱形,
∴AD∥BM,
∴∠DFH=∠M,
在△FDH和△MCH中,‘
$\left\{\begin{array}{l}{∠DFH=∠M}\\{∠FHD=∠CHM}\\{DH=HC}\end{array}\right.$,
∴△FDH≌△MCH,
∴FH=HM,
∵FE⊥BC,
∴∠FEM=90°,
∴EH=FH=HM,
∴EH=FH.
(2)解:如圖2中,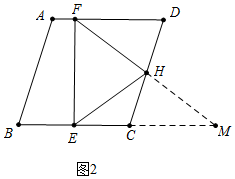
①當(dāng)FD=FH時(shí),設(shè)∠M=∠DFH=x,
∵BE=EC,CH=DH,BC=CD,
∴EC=CH,
∴∠CEH=∠CHE,
∵HE=HM,
∴∠CEH=∠CHE=∠M=x,
∴∠HCM=∠ECH+∠EHC=2x=∠D=∠FHD,
∵∠DFH+∠D+∠FHD=180°,
∴x+2x+2x=180°,
∴5x=180°,
∴x=36°,
∴∠D=72°.
②當(dāng)∠D=90°時(shí),易知DF=DH,△DEF是等腰直角三角形,
綜上所述,當(dāng)△DFH是等腰三角形時(shí),∠D=72°或90°.
點(diǎn)評(píng) 本題考查矩形的性質(zhì)、線段的垂直平分線的性質(zhì)、等腰三角形的判定、直角三角形斜邊中線定理等知識(shí),解題的關(guān)鍵是學(xué)會(huì)分類討論的思想思考問題,屬于中考常考題型.


 高效智能課時(shí)作業(yè)系列答案
高效智能課時(shí)作業(yè)系列答案 捷徑訓(xùn)練檢測(cè)卷系列答案
捷徑訓(xùn)練檢測(cè)卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
| 購票張數(shù) | 1-50張 | 51~100張 | 100張以上 |
| 每張票價(jià) | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
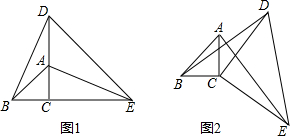
| A. | ②③ | B. | ①④ | C. | 只有③ | D. | ②③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com