
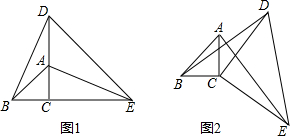
分析 (1)依據(jù)等腰直角三角形的性質(zhì)可得到BC=AC,DC=CE,∠BCD=∠ACE=90°,然后依據(jù)SAS證明△BCD≌△ACE,接下來,依據(jù)全等三角形的性質(zhì)可得到BD=AE;
(2)依據(jù)等腰直角三角形的性質(zhì)可得到BC=AC,DC=CE,∠BCD=∠ACE=90°,然后利用等式的性質(zhì)證明∠BCD=∠ACE,然后依據(jù)SAS證明△BCD≌△ACE,接下來,依據(jù)全等三角形的性質(zhì)可得到BD=AE.
解答 解:(1)∵△BCA和△DCE均為等腰直角三角形,
∴BC=AC,DC=CE,∠BCD=∠ACE=90°.
在△BCD和△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=CE}\end{array}\right.$,
∴△BCD≌△ACE.
∴BD=AE.
(2)成立.
∵△BCA和△DCE均為等腰直角三角形,
∴BC=AC,DC=CE,∠BCD=∠ACE=90°.
∴∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.
在△BCD和△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=CE}\end{array}\right.$,
∴△BCD≌△ACE.
∴BD=AE.
點(diǎn)評 本題主要考查的是全等三角形的性質(zhì)和判定、等腰直角三角形的性質(zhì),熟練掌握相關(guān)知識是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x2-$\frac{1}{x}$=1 | B. | x2+y=2 | C. | $\sqrt{2}$x2=2 | D. | x+5=-7 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
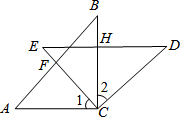 如圖,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB與CE交于F,ED與AB,BC,分別交于M,H.
如圖,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB與CE交于F,ED與AB,BC,分別交于M,H.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
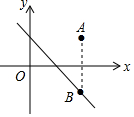 如圖,在平面直角坐標(biāo)系中點(diǎn)A(2,m)在第-象限,若點(diǎn)A關(guān)于x軸的對稱點(diǎn)B在直線y=-x+1上,求m的值.
如圖,在平面直角坐標(biāo)系中點(diǎn)A(2,m)在第-象限,若點(diǎn)A關(guān)于x軸的對稱點(diǎn)B在直線y=-x+1上,求m的值.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -3和6 | B. | -4x2yz和2yzx2 | C. | 2ab2和2a2b | D. | 9a3和-a3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖實(shí)數(shù)在數(shù)軸上表示為:化簡:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.
如圖實(shí)數(shù)在數(shù)軸上表示為:化簡:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
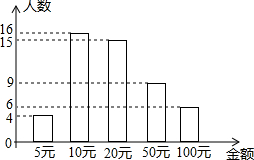 如圖所示是某班50名學(xué)生的捐款情況統(tǒng)計(jì)圖,根據(jù)圖中信息可得捐款金額的中位數(shù)是20元.
如圖所示是某班50名學(xué)生的捐款情況統(tǒng)計(jì)圖,根據(jù)圖中信息可得捐款金額的中位數(shù)是20元.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com