
分析 (1)先設未知數:單獨完成這個路段的施工任務乙工程隊需x天,甲工程隊需$\frac{2}{3}$x天,則甲工程隊的工效為:$\frac{1}{\frac{2x}{3}}$,乙工程隊的工效為:$\frac{1}{x}$,根據甲施工10天,剩下的工程再由甲、乙兩個工程隊合作施工30天完成列方程即可解出;
(2)求設未知數求出乙工程隊還需做45天完成,再設乙工程隊每天施工的費用為a萬元,根據施工費用共計211.5萬元,列方程得出結論;
(3)先根據總工作量÷總工效=總工作時間,計算出需合作36天完成,再根據(2)中的一天的費用:3+2.5=5.5萬元,計算需總費用198萬元,所以不夠用,需補18萬元.
解答 解:(1)設乙工程隊單獨完成這個路段的施工任務需x天,則甲工程隊單獨完成這個路段的施工任務需$\frac{2}{3}$x天,
根據題意得:$\frac{10}{\frac{2x}{3}}$+$\frac{30}{\frac{2x}{3}}$+$\frac{30}{x}$=1,
解得:x=90,
經檢驗:x=90是原方程的解,
當x=90時,$\frac{2}{3}$x=$\frac{2}{3}$×90=60,
答:甲、乙工程隊單獨完成這個路段的施工任務各需60天、90天;
(2)由(1)得:甲工程隊的工效:$\frac{1}{60}$,乙工程隊的工效為:$\frac{1}{90}$,
設甲、乙兩個工程隊共同施工18天后,再由乙工程隊單獨做還需y天完成剩下的施工任務,
則$\frac{18}{60}+\frac{18}{90}+\frac{y}{90}$=1,
解得:y=45,
經檢驗:x=45是原方程的解,
∴甲一共做了18天,乙一共做了18+45=63天,
設乙工程隊每天施工的費用為a萬元,則甲工程隊每天施工的費用為1.2a萬元,
則18×1.2a+63a=211.5,
84.6a=211.5,
a=2.5,
1.2a=1.2×2.5=3,
答:甲工程隊每天施工的費用為3萬元;
(3)若由甲、乙工程隊合作完成,則所需時間為:1÷($\frac{1}{60}$+$\frac{1}{90}$)=36(天)
36×(2.5+3)=198>180,
198-180=18,
答:工程預算費用不夠用,需追加預算18萬元.
點評 本題考查了分式方程的應用,屬于工程問題;明確三個量的關系:總工作量、工作效率、工作時間,熟記總工作量=工作效率×工作時間;列分式方程解應用題一定要審清題意,找相等關系是著眼點,要學會分析題意,提高理解能力,并注意方程要檢驗.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
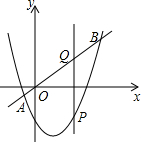 如圖所示,直線y=x與拋物線 y=x2-x-3交于A,B兩點,點P是拋物線上的一個動點,點P作PQ⊥x軸交直線y=x于點Q,設點P的橫坐標為m,則線段PQ的長度隨著m的增大而減小時m的取值范圍是m<-1或1<m<3.
如圖所示,直線y=x與拋物線 y=x2-x-3交于A,B兩點,點P是拋物線上的一個動點,點P作PQ⊥x軸交直線y=x于點Q,設點P的橫坐標為m,則線段PQ的長度隨著m的增大而減小時m的取值范圍是m<-1或1<m<3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
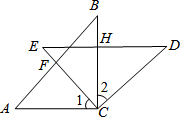 如圖,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB與CE交于F,ED與AB,BC,分別交于M,H.
如圖,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB與CE交于F,ED與AB,BC,分別交于M,H.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com