
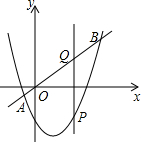
 如圖所示,直線y=x與拋物線 y=x2-x-3交于A,B兩點,點P是拋物線上的一個動點,點P作PQ⊥x軸交直線y=x于點Q,設點P的橫坐標為m,則線段PQ的長度隨著m的增大而減小時m的取值范圍是m<-1或1<m<3.
如圖所示,直線y=x與拋物線 y=x2-x-3交于A,B兩點,點P是拋物線上的一個動點,點P作PQ⊥x軸交直線y=x于點Q,設點P的橫坐標為m,則線段PQ的長度隨著m的增大而減小時m的取值范圍是m<-1或1<m<3. 分析 可用m分別表示出P、Q的坐標,則可用m表示出PQ的長,再利用二次函數的性質可求得答案.
解答 解:
聯立直線和拋物線解析式可得$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}-x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴A(-1,-1),B(3,3),
∵點P在拋物線上,點Q在直線y=x上,且點P的橫坐標為m,
∴P(m,m2-m-3),Q(m,m),
當m<-1或m>3時,可知點P在點Q上方,
∴PQ=m2-m-3-m=m2-2m+4=(m-1)2-4,
∴當m<1時PQ的長度隨m的增大而減小;
當-1<m<3時,可知點Q在點P上方,
∴PQ=m-(m2-m-3)=-m2+2m+3=-(m-1)2+4,
此時拋物線開口向下,對稱軸為m=1,
∴當1<m<3時,PQ隨m的增大而減小,
綜上可知m的取值范圍為:m<-1或1<m<3,
故答案為:m<-1或1<m<3.
點評 本題主要考查二次函數的性質,利用m表示出PQ的長度是解題的關鍵,注意分類討論.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
| 坐姿不良 | 站姿不良 | 走姿不良 | 三姿良好 |
| 100 | 155 | 185 | 60 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 購票張數 | 1-50張 | 51~100張 | 100張以上 |
| 每張票價 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| a | … | 0.000001 | 0.0001 | 0.01 | 1 | 100 | 10000 | 100000 | … |
| $\sqrt{a}$ | … | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com