Question

12．平面直角坐標系中，A（-1，3），C（2，-1），則以AC為對角線的正方形ABCD的頂點B、D坐標分別為多少？

Answer 1

分析 如圖，過點E作FK∥x軸，BF⊥FK于F，DK⊥FK于K，AM⊥FK于M．首先求出點E坐標，推出AM=2，EM=$\frac{3}{2}$，由△AME≌△EKD≌△EFB，可得EK=EF=AM=2，DK=BF=EM=$\frac{3}{2}$，由此即可解決問題．

解答 解：如圖，過點E作FK∥x軸，BF⊥FK于F，DK⊥FK于K，AM⊥FK于M．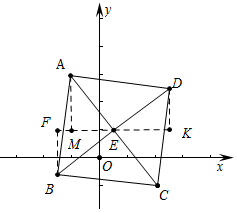

∵四邊形ABCD是正方形，A（-1，3），C（2，-1），
∴EA=EC=EB=ED，E（$\frac{1}{2}$，1），
∴AM=2，EM=$\frac{3}{2}$，
由△AME≌△EKD≌△EFB，可得EK=EF=AM=2，DK=BF=EM=$\frac{3}{2}$，
∴D（$\frac{5}{2}$，$\frac{5}{2}$），B（-$\frac{3}{2}$，-$\frac{1}{2}$）或B（$\frac{5}{2}$，$\frac{5}{2}$），D（-$\frac{3}{2}$，-$\frac{1}{2}$）．

點評 本題考查正方形的性質、全等三角形的判定和性質、中點坐標公式等知識，解題的關鍵是學會添加常用輔助線構造全等三角形解決問題，屬于中考常考題型．