
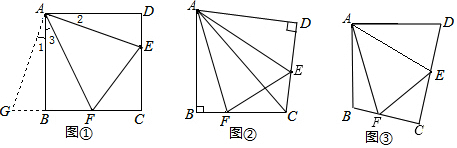
分析 (1)作輔助線,構(gòu)建全等三角形,證明點G,B,F(xiàn)在同一條直線上,再證明△GAF≌△EAF,可得結(jié)論;
(2)同理作輔助線,如圖②,將△ADE繞A順時針旋轉(zhuǎn)∠BAD的度數(shù),此時,AD與AB重合,證明△GAF≌△EAF,同理可以得出EF=BG+BF=DE+BF;
(3)當(dāng)∠B與∠D滿足∠D+∠B=180°時,可使得DE+BF=EF,理由是將△ADE繞A順時針旋轉(zhuǎn)∠BAD的度數(shù),同理證明△GAF≌△EAF,得EF=BG+BF=DE+BF.
解答 解:(1)將△ADE繞點A順時針旋轉(zhuǎn)90°得到△ABG,此時AB與AD重合,由旋轉(zhuǎn)可得:
AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,點G,B,F(xiàn)在同一條直線上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠FAE.
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,故DE+BF=EF.
故答案:FAE,△EAF,GF;
(2)如圖②,DE+BF=EF,理由是: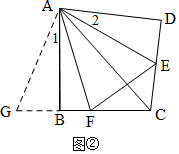
將△ADE繞A順時針旋轉(zhuǎn)∠BAD的度數(shù),此時,AD與AB重合,
由旋轉(zhuǎn)得:BG=DE,∠1=∠2,AE=AG,
∠ABG=∠D=90°,
同理得:點G,B,F(xiàn)在同一條直線上,
∵∠EAF=$\frac{1}{2}$∠DAB,
∴∠BAF+∠EAD=$\frac{1}{2}$∠DAB,
∴∠BAF+∠GAB=$\frac{1}{2}$∠DAB,
∴∠GAF=∠EAF,
∵AE=AG,AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴EF=BG+BF=DE+BF;
(3)當(dāng)∠B與∠D滿足∠D+∠B=180°時,可使得DE+BF=EF,理由是: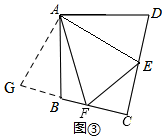
將△ADE繞A順時針旋轉(zhuǎn)∠BAD的度數(shù),此時,AD與AB重合,
由旋轉(zhuǎn)得:BG=DE,∠GAB=∠DAE,AE=AG,
∠ABG=∠D,
∵∠D+∠ABC=180°
∴∠ABC+∠ABG=180°
∴點G,B,F(xiàn)在同一條直線上,
∵∠EAF=$\frac{1}{2}$∠DAB,
∴∠BAF+∠EAD=$\frac{1}{2}$∠DAB,
∴∠BAF+∠GAB=$\frac{1}{2}$∠DAB,
∴∠GAF=∠EAF,
∵AE=AG,AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴EF=BG+BF=DE+BF;
點評 本題是四邊形的綜合題,考查了正方形的性質(zhì)、三角形全等的性質(zhì)和判定,本題運用了類比的思想,通過旋轉(zhuǎn)三角形,利用旋轉(zhuǎn)的性質(zhì)再證明另一對三角形全等,來解決線段的和差問題.


 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 30m | B. | 40m | C. | 50m | D. | 70m |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{2}{{\sqrt{2}}}$ | B. | $\root{3}{2}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 在平面直角坐標(biāo)系xOy中,有一點C,過點C分別作CA⊥x軸,CB⊥y軸,點A、B是垂足.
在平面直角坐標(biāo)系xOy中,有一點C,過點C分別作CA⊥x軸,CB⊥y軸,點A、B是垂足.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -22=4 | B. | |-$\sqrt{2}$|=$\sqrt{2}$ | C. | $\sqrt{4}$=±2 | D. | -|-2|=2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
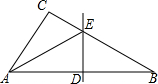 如圖,△ABC中,∠C=90°,邊AB的垂直平分線交AB,AC邊分別為點D,點E,連接BE,若AB=10,BC=6,則△ACE的周長是14.
如圖,△ABC中,∠C=90°,邊AB的垂直平分線交AB,AC邊分別為點D,點E,連接BE,若AB=10,BC=6,則△ACE的周長是14.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com