
 在平面直角坐標系xOy中,有一點C,過點C分別作CA⊥x軸,CB⊥y軸,點A、B是垂足.
在平面直角坐標系xOy中,有一點C,過點C分別作CA⊥x軸,CB⊥y軸,點A、B是垂足.分析 (1)計算1×2≠2×(|-1|+2),4×4=2×(4+4)即可求得答案;
(2)①(4+m)×2=4m,可求出m,把N點坐標代入一次函數(shù)解析式可求得b;②由一次函數(shù)解析式可求得D點坐標,則可求得△OND的面積,由條件則可求得點M到y(tǒng)軸的距離,則可求得M點的坐標;
(3)可設Q點坐標為(x,-2),由平衡點的定義可得到關于x的方程,解方程進行判斷即可.
解答 解:
(1)∵1×2≠2×(|-1|+2),4×4=2×(|-4|+4),
∴點E不是平衡點,點N是平衡點,
故答案為:②;
(2)①∵N是第一象限中的平衡點,
∴4m=2(4+m),解得m=4,
∴N(4,4),
∵N點在y=-x+b的圖象上,
∴4=-4+b,解得b=8;
②由①可知一次函數(shù)解析式為y=-x+8,
∴D(0,8),
∴OD=8,且N(4,4),
∴S△OND=$\frac{1}{2}$×4×8=16,
∴S△OMD=3S△OND=3×16=48,
設M坐標為(t,-t+8),則M到y(tǒng)軸的距離為|t|,
∴$\frac{1}{2}$×8×|t|=48,解得t=12或t=-12,
當t=12時,-t+8=-4,當t=-12時,-t+8=20,
∴存在滿足條件的點M,其坐標為(12,-4)或(-12,20);
(3)∵PQ∥x軸,且P(0,-2),
∴可設點Q坐標為(x,-2),
∵點Q為平衡點,
∴2|x|=2(|x|+2),該方程無解,
∴不存在滿足條件的Q點.
點評 本題為一次函數(shù)的綜合應用,涉及待定系數(shù)法、三角形面積、新定義、分類討論及方程思想等知識點.解決本題的關鍵是理解題目中所給的平衡點的定義.本題考查知識點不多,難度不大.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:選擇題
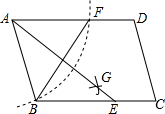 如圖,用直尺和圓規(guī)作∠BAD的平分線AG,過點B作BC∥AD,交AG于點E,BF=6,AB=5,則AE的長為( )
如圖,用直尺和圓規(guī)作∠BAD的平分線AG,過點B作BC∥AD,交AG于點E,BF=6,AB=5,則AE的長為( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 拋物線y=x2+4ax+b與x軸相交于O、A兩點(其中O為坐標原點),過點P(2,2a)作直線PM⊥x軸于點M,交拋物線于點B,點B關于拋物線對稱軸的對稱點為C(其中B、C不重合),連接AP交y軸于點N,連接BC和PC.
拋物線y=x2+4ax+b與x軸相交于O、A兩點(其中O為坐標原點),過點P(2,2a)作直線PM⊥x軸于點M,交拋物線于點B,點B關于拋物線對稱軸的對稱點為C(其中B、C不重合),連接AP交y軸于點N,連接BC和PC.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com