
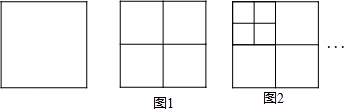
分析 (1)(1)由第一次可得5個正方形,第二次可得9個正方形,第三次可得13個正方形,可得規律:第n次可得(4n+1)個正方形;
(2)此題可看作上面幾何體面積問題,即可求得答案.
解答 解:我選擇第A題,
故答案為:A,
(1)∵第一次可得5個正方形,第二次可得9個正方形,第三次可得13個正方形,
∴第n次可得(4n+1)個正方形,
故答案為:4n+1;
(2)根據題意得:原式=(1-$\frac{1}{4}$)+($\frac{1}{4}$-$\frac{1}{{4}^{2}}$)+($\frac{1}{{4}^{2}}$-$\frac{1}{{4}^{3}}$)+…+($\frac{1}{{4}^{n-1}}$-$\frac{1}{{4}^{n}}$)=1-$\frac{1}{{4}^{n}}$,
故答案為:1-$\frac{1}{{4}^{n}}$.
點評 此題考查了規律問題.注意根據題意得到規律:第n次可得(4n+1)個正方形是解此題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1500元 | B. | 1400元 | C. | 1300元 | D. | 1200元 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
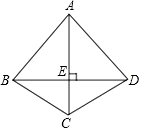 如圖,四邊形ABCD中,AC垂直平分BD,垂足為E,下列結論不一定成立的是( )
如圖,四邊形ABCD中,AC垂直平分BD,垂足為E,下列結論不一定成立的是( )| A. | AC平分∠BCD | B. | AB=BD | C. | △BEC≌△DEC | D. | BC=DC |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
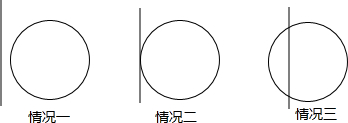
 如圖,⊙C過原點,與x軸、y軸分別交于A、D兩點,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半徑是2,則OD的長為2$\sqrt{3}$.
如圖,⊙C過原點,與x軸、y軸分別交于A、D兩點,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半徑是2,則OD的長為2$\sqrt{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com