Question

17．人工浮床又稱人工浮島，自20年前人類開發出第一個人工浮床之后，就將人工浮床應用于地表水體的污染治理和生態修復．近年來，我國的人工浮床技術開發及用于正好處于快速發展時期．如圖所示，是我市在某湖面上為凈化水質而搭建的一個水上圓形人工浮床示意圖，其中圓和三塊邊長為16米的正方形是浮島框架部分，被分割成的7部分將運用無土技術分別栽培7種不同的水生植物，正方形的頂點A、B、C、D都在圓上，且整個浮床成軸對稱圖形，求這個圓形人工浮床的半徑．

Answer 1

分析 連接BD交EF于P，過P作PO⊥BD交HG于O，連接OB，根據全等三角形的性質得到PB=PE，由垂徑定理得到點O為圓心，根據勾股定理得到BD=$\sqrt{3{2}^{2}+2{4}^{2}}$=40，得到PB=20，得到PH=4，根據相似三角形的性質得到HO=3，根據勾股定理即可得到結論．

解答 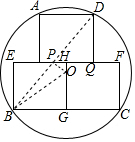解：連接BD交EF于P，過P作PO⊥BD交HG于O，連接OB，
在△BEP與△PDQ中，$\left\{\begin{array}{l}{∠E=∠DQP}\\{∠EPB=∠EPQ}\\{BE=EQ}\end{array}\right.$，
∴△BEP≌△DQP，
∴PB=PD，
∴點O為圓心，
∵BD=$\sqrt{3{2}^{2}+2{4}^{2}}$=40，
∴PB=20，
∴PE=$\sqrt{P{B}^{2}-B{E}^{2}}$=12，
∴PH=4，
∵∠E=∠EHG=90°，
∴∠EBP+∠EPB=∠EPB+∠HPO=90°，
∴∠EPB=∠HPO，
∴△PBE∽△POH，
∴$\frac{PH}{BE}=\frac{HO}{PE}$，
∴HO=3，
∴OG=13，
∴OB=$\sqrt{B{G}^{2}+O{G}^{2}}$=5$\sqrt{17}$，
∴這個圓形人工浮床的半徑為5$\sqrt{17}$米．

點評 本題考查了全等三角形的判斷和性質，垂徑定理的應用，軸對稱圖形的性質，相似三角形的判定和性質，正方形的性質，正確的作出輔助線是解題的關鍵．