Question

17．如圖在平面直角坐標系中，直線l₁：y=-$\frac{1}{2}$x+3與x軸交于點A，與y軸交于點B，直線l₂：y=kx+2k與x軸交于點C，與直線l₁交于點P．
（1）直線l₂是否經過x軸上一定點？若經過，請直接寫出定點坐標；若不經過，請說明理由；
（2）若S_△ACP=8，求直線l₂的函數關系式；
（3）過點M（0，6）作平行于x軸的直線l₃，點Q為直線l₃上一個動點，當△QAB為等腰三角形時，求所有點Q的坐標．

Answer 1

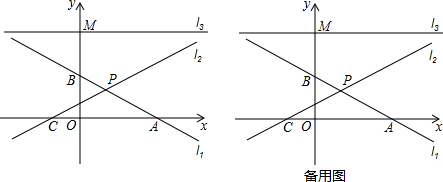
分析 （1）由y=kx+2k得到y=k（x+2），無論k取何值時，當x=-2時，y=0，故此直線y=kx+2k經過x軸上定點（-2，0）；
（2）令y₁=0得到-$\frac{1}{2}$x+3=0，解得x=6，故此A（6，0），由（1）可知點C的坐標為（-2，0），故此AC=8，由三角形的面積公式可知P_y=2，將y=2代入y=-$\frac{1}{2}×$+3，求得x=2，于是得到點P的坐標為（2，2），將點P的坐標代入y=kx+2k可求得k的值；
（3）將x=0代入y=-$\frac{1}{2}$x+3得到y=3，從而得到點B的坐標為（0，3），設點Q的坐標為（n，6），分別根據QB=QA；BQ=BA；AB=AQ以及兩點間的距離公式列出關于n的方程，從而可解得n的值．

解答 解：（1）∵y=kx+2k，
∴y=k（x+2）．
∴當x=-2時，y=0．
∴直線L₂經過點（-2，0）．
（2）∵令y₁=0得到-$\frac{1}{2}$x+3=0，解得x=6，
∴A（6，0）．
∵由（1）可知：點C的坐標為（-2，0）．
∴AC=8．
∵S_△ACP=8，
∴$\frac{1}{2}×AC×{P}_{y}$=8，即$\frac{1}{2}×8×{P}_{y}$=8．
解得：P_y=2．
∵將y=2代入-$\frac{1}{2}$x+3=0得：-$\frac{1}{2}$x+3=2，解得x=2，
∴點P的坐標為（2，2）．
將點P的坐標代入y=kx+2k得：2k+2k=2，解得：k=$\frac{1}{2}$．
∴直線L₂的解析式為$y=\frac{1}{2}x+1$．
（3）∵將x=0代入y=-$\frac{1}{2}$x+3得：y=3，
∴點B的坐標為（0，3）．
設點Q的坐標為（n，6）．
①當QB=QA時，由兩點間的距離公式得：n²+（6-3）²=（6-n）²+（6-0）²．
解得：n=$\frac{21}{4}$．
∴點Q的坐標為（$\frac{21}{4}$，6）．
②當BQ=BA時，由兩點間的距離公式得：n²+（6-3）²=（6-0）²+（3-0）²．
解得：n=6或n-6．
∴點Q的坐標為（6，6）或（-6，6）．
∵將Q（-6，6）代入y=-$\frac{1}{2}x+3$得：y=-$\frac{1}{2}×$（-6）+3=6，
∴點Q在直線AB上，此時A、B、Q不能構成三角形．
∴Q（-6，6）（舍去）．
∴點Q的坐標為（6，6）．
③當AB=AQ時，由兩點間的距離公式得：（n-6）²+（6-0）²=（6-0）²+（3-0）²．
解得：n=9或n=3．
∴點Q的坐標為（9，6）或（3，6）．
綜上所述，點Q的坐標為（9，6）或（3，6）或（6，6）或（$\frac{21}{4}，6$）．

點評 本題主要考查的是一次函數的綜合應用，解答本題主要應用了待定系數法求一次函數的解析式、一次函數圖象上點的坐標特點、兩點間的距離公式、等腰三角形的性質、三角形的面積公式，根據兩點間的距離公式列出關于n的方程是解題的關鍵．