
 如圖,坐標平面上,△ABC與△DEF全等,其中A、B、C的對應頂點分別為D、E、F,且AB=BC=10,A點的坐標為(-6,2),B、C兩點在方程式y=-6的圖形上,D、E兩點在y軸上,則F點的縱坐標為2,則直線EF解析式為y=$\frac{3}{4}$x-4.
如圖,坐標平面上,△ABC與△DEF全等,其中A、B、C的對應頂點分別為D、E、F,且AB=BC=10,A點的坐標為(-6,2),B、C兩點在方程式y=-6的圖形上,D、E兩點在y軸上,則F點的縱坐標為2,則直線EF解析式為y=$\frac{3}{4}$x-4. 分析 如圖,作輔助線;證明△AKC≌△CHA,即可求得CK=AH=8,證明∠BAC=∠EDF,AC=DF,進而證明△AKC≌△DPF,即可求得E、F點的坐標,然后根據待定系數法即可求得解析式.
解答 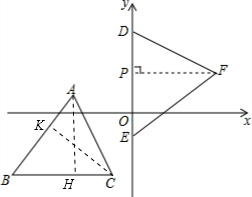 解:如圖,在△ABC中,分別作高線AH、CK,則∠AKC=∠CHA.
解:如圖,在△ABC中,分別作高線AH、CK,則∠AKC=∠CHA.
∵AB=BC,
∴∠BAC=∠BCA.
在△AKC和△CHA中,
$\left\{\begin{array}{l}{∠AKC=∠CHA}\\{∠BAC=∠BCA}\\{AC=CA}\end{array}\right.$,
∴△AKC≌△CHA(AAS),
∴CK=AH.
∵A點的坐標為(-6,2),
B、C兩點的縱坐標均為-6,
∴AH=8.
又∵CK=AH,
∴CK=AH=8.
∵AB=BC=10,
∴BK=$\sqrt{B{C}^{2}-C{K}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴AK=10-6=4,
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,DE=AB=10.
在△AKC和△DPF中,
$\left\{\begin{array}{l}{∠AKC=∠DPF}\\{∠BAC=∠EDF}\\{AC=DF}\end{array}\right.$,
∴△AKC≌△DPF(AAS),
∴PF=KC=8,DP=AK=4.
∴PE=10-4=6,
∵F點的縱坐標為2,
∴E(0,-4),F(8,2),
設直線EF的解析式為y=kx-4,
代入F(8,2)得,2=8k-4,
解得k=$\frac{3}{4}$,
∴直線EF解析式為y=$\frac{3}{4}$x-4.
故答案為y=$\frac{3}{4}$x-4.
點評 該題主要考查了全等三角形的判定及其性質以及待定系數法求一次函數的解析式;解題的關鍵是作輔助線,構造全等三角形,靈活運用全等三角形的判定及其性質來分析、判斷、推理或解答.


科目:初中數學 來源: 題型:解答題
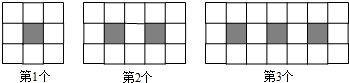
| 序號 | 1 | 2 | 3 | … |
圖形 | x x y x x | x x x y y x x y y x x x | x x x x y y y x x y y y x x y y y x x x x | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,數軸上有A、B、C、O四點,點O是原點,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如圖,數軸上有A、B、C、O四點,點O是原點,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
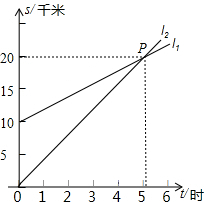 如圖,l1反映了甲離開A地的時間與離A地的距離的關系l2反映了乙離開A地的時間與離開A地距離之間的關系,根據圖象填空:
如圖,l1反映了甲離開A地的時間與離A地的距離的關系l2反映了乙離開A地的時間與離開A地距離之間的關系,根據圖象填空:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 數量范圍(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 價格(元) | 零售價的95% | 零售價的85% | 零售價的75% | 零售價的70% |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com