
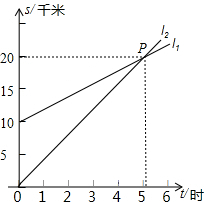
 如圖,l1反映了甲離開A地的時間與離A地的距離的關系l2反映了乙離開A地的時間與離開A地距離之間的關系,根據(jù)圖象填空:
如圖,l1反映了甲離開A地的時間與離A地的距離的關系l2反映了乙離開A地的時間與離開A地距離之間的關系,根據(jù)圖象填空:分析 (1)由圖象可以得到當時間為0時,甲離A地的距離是多少;
(2)由圖象可以得到甲、乙兩人離A地距離相等時的時間;
(3)由圖象可以得到點P的坐標;
(4)設出l1對應的函數(shù)表達式,然后根據(jù)點(0,10),(5,20)在此函數(shù)的圖象上,可以求得相應的函數(shù)解析式;
(5)將t=2代入l1的函數(shù)解析式,可以求得S1的值,從而可以解答本題;
(6)設出l2對應的函數(shù)表達式,然后根據(jù)點(5,20)在此函數(shù)的圖象上,可以求得l2對應的函數(shù)表達式,然后令S2=28,可以求得相應的t的值,本題得以解決.
解答 解:(1)由圖象可知,當時間為0時,甲離A地10千米,
故答案為:10;
(2)由圖象可知,當時間等于5時,甲、乙兩人離A地距離相等;
故答案為:5;
(3)由圖象可得,點P的坐標為(5,20);
故答案為:(5,20);
(4)設l1對應的函數(shù)表達式是:S1=kt+b,
∵點(0,10),(5,20)在此函數(shù)的圖象上,
∴$\left\{\begin{array}{l}{10=b}\\{20=5k+b}\end{array}\right.$
解得,k=2,b=10
即l1對應的函數(shù)表達式是:S1=2t+10,
故答案為:2t+10;
(5)當t=2時,S1=2×2+10=14千米,
故答案為:14;
(6)設l2對應的函數(shù)表達式是:S2=mt,
∵點(5,20)在此函數(shù)的圖象上,
∴20=5m,
解得,m=4,
即l2對應的函數(shù)表達式是:S2=4t,
令S2=28時,28=4t,得t=7,
故答案為:7.
點評 本題考查一次函數(shù)的應用,解題的關鍵是明確題意,利用數(shù)形結合的思想解答問題.


科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 (1)已知一個角是它的余角的一半,求這個角的度數(shù);
(1)已知一個角是它的余角的一半,求這個角的度數(shù);查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖,坐標平面上,△ABC與△DEF全等,其中A、B、C的對應頂點分別為D、E、F,且AB=BC=10,A點的坐標為(-6,2),B、C兩點在方程式y(tǒng)=-6的圖形上,D、E兩點在y軸上,則F點的縱坐標為2,則直線EF解析式為y=$\frac{3}{4}$x-4.
如圖,坐標平面上,△ABC與△DEF全等,其中A、B、C的對應頂點分別為D、E、F,且AB=BC=10,A點的坐標為(-6,2),B、C兩點在方程式y(tǒng)=-6的圖形上,D、E兩點在y軸上,則F點的縱坐標為2,則直線EF解析式為y=$\frac{3}{4}$x-4.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
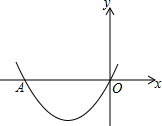 如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.
如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 一種長方形餐桌的四周可坐6人用餐,現(xiàn)把若干張這樣的餐桌按如圖方式進行拼接.那么需要多少張餐桌拼在一起可坐90人用餐?若設需要這樣的餐桌x張,可列方程為4x+2=90.
一種長方形餐桌的四周可坐6人用餐,現(xiàn)把若干張這樣的餐桌按如圖方式進行拼接.那么需要多少張餐桌拼在一起可坐90人用餐?若設需要這樣的餐桌x張,可列方程為4x+2=90.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖所示,兩個四邊形均為正方形,正方形ABCD邊長為a,正方形CGFE邊長為5.
如圖所示,兩個四邊形均為正方形,正方形ABCD邊長為a,正方形CGFE邊長為5.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com