
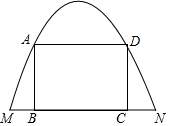
 有一如圖所示的紙片,拱形邊緣呈拋物線形形狀,MN=8米,拋物線頂點到邊MN的距離是8米.點A和點D是拋物線上的兩動點,且AD∥BC,過點A作AB⊥BC作DC⊥BC,過點B作DC⊥BC,點B、C在邊MN上.
有一如圖所示的紙片,拱形邊緣呈拋物線形形狀,MN=8米,拋物線頂點到邊MN的距離是8米.點A和點D是拋物線上的兩動點,且AD∥BC,過點A作AB⊥BC作DC⊥BC,過點B作DC⊥BC,點B、C在邊MN上.分析 (1)以MN所在直線為x軸、MN的中垂線為y軸建立平面直角坐標系,待定系數法求出函數解析式,設OC=a,則CD=-$\frac{1}{2}$a2+8,若四邊形ABCD是正方形,由題意知四邊形ABCD是矩形,則CD=2OC,據此列出關于a的方程,解之得出a的值,即可得答案;
(2)設矩形ABCD的周長為L,OC=a,則CD=-$\frac{1}{2}$a2+8,根據矩形的周長公式列出函數解析式并配方,從而由二次函數的性質可得答案.
解答 解:(1)能成為正方形,
如圖,以MN所在直線為x軸、MN的中垂線為y軸建立平面直角坐標系,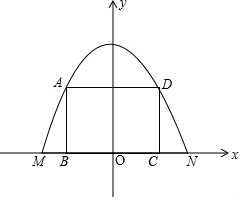
則該拋物線的頂點坐標為(0,8)、點M(-4,0)、N(4,0),
設解析式為y=ax2+8,
將點N(4,0)代入得:16a+8=0,
解得:a=-$\frac{1}{2}$,
∴y=-$\frac{1}{2}$x2+8,
∵AD∥BC,AB⊥BC,DC⊥BC,
∴四邊形ABCD是矩形,
若四邊形ABCD是正方形,
則CD=2OC,
設OC=a,則CD=-$\frac{1}{2}$a2+8,
∴-$\frac{1}{2}$a2+8=2a,
解得:a=-2-2$\sqrt{5}$<-4(舍),a=-2+2$\sqrt{5}$<4(符合題意),
故四邊形ABCD可以是正方形.
(2)由(1)知,設矩形ABCD的周長為L,OC=a,則CD=-$\frac{1}{2}$a2+8,
∴L=4a+2(-$\frac{1}{2}$a2+8)=-a2+4a+16=-(a-2)2+20,
故當a=2時,L最大=20,
答:矩形ABCD的周長為20.
點評 本題主要考查二次函數的實際應用和正方形的判定,根據題意建立合適的平面直角坐標系并利用待定系數法求得函數解析式、根據正方形的判定得出關于a的方程和矩形周長公式列出函數解析式是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
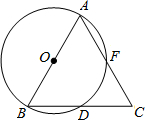 如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD到點C,使DC=BD,連結AC交⊙O于點F.
如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD到點C,使DC=BD,連結AC交⊙O于點F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com