
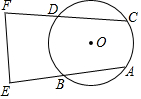
 如圖,已知在⊙O中,弦AB=CD,延長AB到E,延長CD到F,使BE=DF,求證:EF的垂直平分線經過點O.
如圖,已知在⊙O中,弦AB=CD,延長AB到E,延長CD到F,使BE=DF,求證:EF的垂直平分線經過點O. 分析 過點O作OG⊥CF于點G,OH⊥AE于點H,由垂徑定理和勾股定理可知OH=OG,OE=OF,然后利用勾股定理證明OE=OF,由等腰三角形的性質可知EF的垂直平分線必過O點.
解答 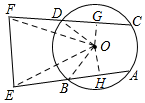 解:過點O作OG⊥CF于點G,OH⊥AE于點H,連接OF、OE,
解:過點O作OG⊥CF于點G,OH⊥AE于點H,連接OF、OE,
∴由垂徑定理可知:BH=$\frac{1}{2}$AB,DG=$\frac{1}{2}$CD,
∵AB=CD,
∴BH=DG,
∵OD=OB,
∴由勾股定理可知:OG2=OH2,
∵BE=DF,
∴BE+BH=DF+DG,
∴EH=FG,
∴在Rt△OEH與Rt△OFG中,
由勾股定理可知:OE2=OF2,
∴OE=OF,
∴△OFE是等腰三角形,
∴由等腰三角形的三線合一可知:EF的垂直平分線過O點.
點評 本題考查垂徑定理,涉及勾股定理,等腰三角形的性質,解題的關鍵是證明△OEF是等腰三角形,然后利用三線合一說明EF的垂直平分線經過點O,本題屬于基礎題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
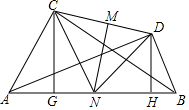 已知:如圖,∠ACB=∠ADB=90°,M、N分別是CD、AB的中點,連結CN、DN,過點C作CG⊥AB,過點D作DH⊥AB,恰好有CG=NH.
已知:如圖,∠ACB=∠ADB=90°,M、N分別是CD、AB的中點,連結CN、DN,過點C作CG⊥AB,過點D作DH⊥AB,恰好有CG=NH.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
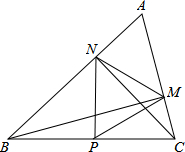 如圖,在△ABC中∠A=60°,BM⊥AC于點M,CN⊥AB于點N,P為BC邊的中點,連接PM.PN.
如圖,在△ABC中∠A=60°,BM⊥AC于點M,CN⊥AB于點N,P為BC邊的中點,連接PM.PN.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
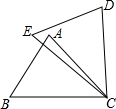 如圖,在△ABC和△DEC中,已知BC=EC,∠B=∠E,還需添加一個條件才能使△ABC≌△DEC,不能添加的一個條件是( )
如圖,在△ABC和△DEC中,已知BC=EC,∠B=∠E,還需添加一個條件才能使△ABC≌△DEC,不能添加的一個條件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com