
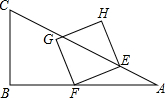
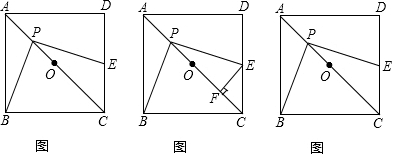
 如圖,在△ABC中,∠B=90°,AB=4,BC=2,點E從點A出發,以每秒$\sqrt{5}$個單位長度的速度沿邊AC向終點C運動,E點出發的同時,點F從點B出發,以每秒2個單位長度的速度沿邊BA向終點A運動,連結EF,將線段EF繞點F逆時針旋轉90°得到線段FG,以EF、FG為邊作正方形EFGH,設點F運動的時間為t秒(t>0)
如圖,在△ABC中,∠B=90°,AB=4,BC=2,點E從點A出發,以每秒$\sqrt{5}$個單位長度的速度沿邊AC向終點C運動,E點出發的同時,點F從點B出發,以每秒2個單位長度的速度沿邊BA向終點A運動,連結EF,將線段EF繞點F逆時針旋轉90°得到線段FG,以EF、FG為邊作正方形EFGH,設點F運動的時間為t秒(t>0)分析 (1)作垂線段ED,根據三角函數求DE的長,即是點E到邊AB的距離;
(2)當點G落在邊AB上時,如圖2,此時EF⊥AB,根據同角的三角函數列式可求得t的值;
(3)分兩種情況:①當0≤t≤1時,如圖3,作高線GP,根據△GPF≌△FDE,則GP=DF=4-4t,代入面積公式求S即可;②當1<t≤2時,如圖4,同理作高線求出結論;
(4)當E與C重合,F與A重合時,AH=CG,則t=2.
解答 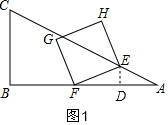 解:(1)如圖1,過E作ED⊥AB于D,
解:(1)如圖1,過E作ED⊥AB于D,
由題意得:AE=$\sqrt{5}t$,
Rt△ABC中,由勾股定理得:AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
sin∠A=$\frac{DE}{AE}$=$\frac{BC}{AC}$,
∴$\frac{DE}{\sqrt{5}t}$=$\frac{2}{2\sqrt{5}}$,
∴DE=t,
則點E到邊AB的距離是t;
(2)當點G落在邊AB上時,如圖2,此時EF⊥AB,
由(1)得:EF=t,
∵BF=2t,
∴AF=4-2t,
tan∠A=$\frac{BC}{AB}$=$\frac{EF}{AF}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴$\frac{t}{4-2t}$=$\frac{1}{2}$,
t=1;
(3)分兩種情況:
①當0≤t≤1時,如圖3,過E作ED⊥AB于D,過G作GP⊥AB于P,
∵ED=t,AD=2t,BF=2t,
∴FD=4-4t,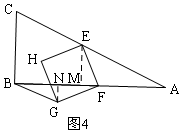
易證△GPF≌△FDE,
∴GP=DF=4-4t,
∴S=S△BFG=$\frac{1}{2}$BF•GP=$\frac{1}{2}×2t$×(4-4t)=-4t2+4t(0≤t≤1);
②當1<t≤2時,如圖4,過E作EM⊥BC于M,過G作GN⊥BC于N,
易證△EMF≌△FNG,
∴GN=FM,
∴EM=t,AM=2t,
∴BM=4-2t,
∴FM=GN=2t-(4-2t)=4t-4,
∴S=S△BFG=$\frac{1}{2}$BF•GN=$\frac{1}{2}×2t$×(4t-4)=4t2-4t(1<t≤2);
綜上所述,S與t之間的函數關系式為:
S=$\left\{\begin{array}{l}{-4{t}^{2}+4t(0≤t≤1)}\\{4{t}^{2}-4t(1<t≤2)}\end{array}\right.$;
(4)正方形EFGH的頂點H,G分別與點A,C距離相等時,如圖5,此時E與C重合,F與A重合,
∴t=2.
點評 本題是四邊形的綜合題,考查了正方形的性質、全等三角形的判定和性質、勾股定理的運用以及三角形面積的求法等知識點.試題難度不大,需要注意的是(3)問中,在兩動點運動過程中,△BFG的面積符合一個函數關系式,本題的關鍵是用含時間的代數式準確表示BF和AE的長度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | a $\sqrt{12ab}$ | B. | 12a2b | C. | a2$\sqrt{12b}$ | D. | 2a $\sqrt{3b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,甲、乙兩盞路燈相距20米,一天晚上,當小剛從燈甲底部向燈乙底部直行16米時,發現自己的身影頂部正好接觸到路燈乙的底部.已知小剛的身高為1.6米,那么路燈甲的高為8米.
如圖,甲、乙兩盞路燈相距20米,一天晚上,當小剛從燈甲底部向燈乙底部直行16米時,發現自己的身影頂部正好接觸到路燈乙的底部.已知小剛的身高為1.6米,那么路燈甲的高為8米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 62500 | B. | 1000 | C. | 500 | D. | 250 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 有兩個十分喜歡探究的同學小明和小芳,他們善于將所做的題目進行歸類,下面是他們的探究過程.
有兩個十分喜歡探究的同學小明和小芳,他們善于將所做的題目進行歸類,下面是他們的探究過程.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com