
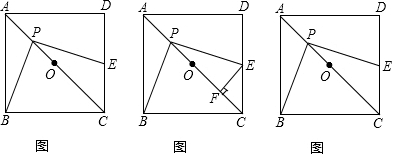
分析 (1)作輔助線,構(gòu)建全等三角形,根據(jù)ASA證明△BMP≌△PNE可得結(jié)論;
(2)如圖2,連接OB,通過證明△OBP≌△FPE,得PF=OB,則PF為定值是$\sqrt{2}$;
(3)根據(jù)△AMP和△PCN是等腰直角三角形,得PA=$\sqrt{2}$PM,PC=$\sqrt{2}$NC,整理可得結(jié)論.
解答 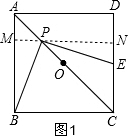 證明:(1)如圖1,過P作MN∥AD,交AB于M,交CD于N,
證明:(1)如圖1,過P作MN∥AD,交AB于M,交CD于N,
∵PB⊥PE,
∴∠BPE=90°,
∴∠MPB+∠EPN=90°,
∵四邊形ABCD是正方形,
∴∠BAD=∠D=90°,
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D=90°,
∴∠MPB+∠MBP=90°,
∴∠EPN=∠MBP,
Rt△PNC中,∠PCN=45°,
∴△PNC是等腰直角三角形,
∴PN=CN,
∵∠BMP=∠PNC=∠ABC=90°,
∴四邊形MBCN是矩形,
∴BM=CN,
∴BM=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE;
(2)在P點(diǎn)運(yùn)動(dòng)的過程中,PF的長度不發(fā)生變化,理由是:
如圖2,連接OB,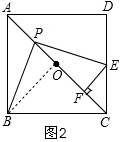
∵點(diǎn)O是正方形ABCD對(duì)角線AC的中點(diǎn),
∴OB⊥AC,
∴∠AOB=90°,
∴∠AOB=∠EFP=90°,
∴∠OBP+∠BPO=90°,
∵∠BPE=90°,
∴∠BPO+∠OPE=90°,
∴∠OBP=∠OPE,
由(1)得:PB=PE,
∴△OBP≌△FPE,
∴PF=OB,
∵AB=2,△ABO是等腰直角三角形,
∴OB=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴PF為定值是$\sqrt{2}$;
(3)如圖1,PC=PA+$\sqrt{2}$EC,理由是:
∵∠BAC=45°,
∴△AMP是等腰直角三角形,
∴PA=$\sqrt{2}$PM,
由(1)知:PM=NE,
∴PA=$\sqrt{2}$NE,
∵△PCN是等腰直角三角形,
∴PC=$\sqrt{2}$NC=$\sqrt{2}$(NE+EC)=$\sqrt{2}$NE+$\sqrt{2}$EC=PA+$\sqrt{2}$EC.
點(diǎn)評(píng) 本題是一個(gè)動(dòng)態(tài)幾何題,考查用正方形性質(zhì)、等腰直角三角形的性質(zhì)、三角形全等的條件和性質(zhì)進(jìn)行有條理的思考和表達(dá)能力.利用條件構(gòu)造三角形全等是解題的關(guān)鍵.本題涉及知識(shí)點(diǎn)較多,綜合性很強(qiáng),難度適中.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
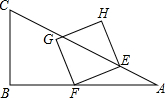 如圖,在△ABC中,∠B=90°,AB=4,BC=2,點(diǎn)E從點(diǎn)A出發(fā),以每秒$\sqrt{5}$個(gè)單位長度的速度沿邊AC向終點(diǎn)C運(yùn)動(dòng),E點(diǎn)出發(fā)的同時(shí),點(diǎn)F從點(diǎn)B出發(fā),以每秒2個(gè)單位長度的速度沿邊BA向終點(diǎn)A運(yùn)動(dòng),連結(jié)EF,將線段EF繞點(diǎn)F逆時(shí)針旋轉(zhuǎn)90°得到線段FG,以EF、FG為邊作正方形EFGH,設(shè)點(diǎn)F運(yùn)動(dòng)的時(shí)間為t秒(t>0)
如圖,在△ABC中,∠B=90°,AB=4,BC=2,點(diǎn)E從點(diǎn)A出發(fā),以每秒$\sqrt{5}$個(gè)單位長度的速度沿邊AC向終點(diǎn)C運(yùn)動(dòng),E點(diǎn)出發(fā)的同時(shí),點(diǎn)F從點(diǎn)B出發(fā),以每秒2個(gè)單位長度的速度沿邊BA向終點(diǎn)A運(yùn)動(dòng),連結(jié)EF,將線段EF繞點(diǎn)F逆時(shí)針旋轉(zhuǎn)90°得到線段FG,以EF、FG為邊作正方形EFGH,設(shè)點(diǎn)F運(yùn)動(dòng)的時(shí)間為t秒(t>0)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 絕對(duì)值最小的實(shí)數(shù)是0 | B. | 立方根最小的實(shí)數(shù)是0 | ||
| C. | 平方最小的實(shí)數(shù)是0 | D. | 算術(shù)平方根最小的實(shí)數(shù)是0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
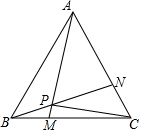 如圖,等邊△ABC的邊長是6,動(dòng)點(diǎn)M、N分別同時(shí)從B、C出發(fā),沿邊BC、CA以1個(gè)單位/秒的速度運(yùn)動(dòng)(動(dòng)點(diǎn)M、N分別到達(dá)C、A時(shí)停止運(yùn)動(dòng)),AM、BN交于點(diǎn)P,運(yùn)動(dòng)時(shí)間是t秒.
如圖,等邊△ABC的邊長是6,動(dòng)點(diǎn)M、N分別同時(shí)從B、C出發(fā),沿邊BC、CA以1個(gè)單位/秒的速度運(yùn)動(dòng)(動(dòng)點(diǎn)M、N分別到達(dá)C、A時(shí)停止運(yùn)動(dòng)),AM、BN交于點(diǎn)P,運(yùn)動(dòng)時(shí)間是t秒.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com