
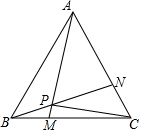
 如圖,等邊△ABC的邊長是6,動點M、N分別同時從B、C出發,沿邊BC、CA以1個單位/秒的速度運動(動點M、N分別到達C、A時停止運動),AM、BN交于點P,運動時間是t秒.
如圖,等邊△ABC的邊長是6,動點M、N分別同時從B、C出發,沿邊BC、CA以1個單位/秒的速度運動(動點M、N分別到達C、A時停止運動),AM、BN交于點P,運動時間是t秒.分析 (1)①軌跡等邊三角形的性質、全等三角形的判定定理證明△ABM≌△BCN,得到AM=BN;
②根據全等三角形的性質、三角形的外角的性質計算即可;
(2)根據圓內接四邊形的判定和性質得到∠MNC=∠MPC=90°,根據∠NCM=60°列出方程,解方程即可;
(3)根據題意確定點P運動的路徑長,根據弧長公式計算即可.
解答 解:(1)①由題意得,BM=CN,∠ABC=∠ACB=60°,
在△ABM和△BCN中,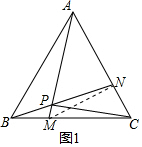
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠BCN}\\{BM=CN}\end{array}\right.$,
∴△ABM≌△BCN,
∴AM=BN;
②∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BPM=∠ABP+∠BAM=∠ABP+∠CBN=60°;
(2)連接MN,
∵∠APN=∠ACM=60°,
∴P、M、C、N四點共圓,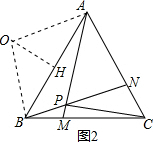
∴∠MNC=∠MPC=90°,
∵∠NCM=60°,
∴MC=2CN,即6-t=2t,
解得,t=2,
答:當PC⊥AM時,t=2;
(3)∵∠BPM=60°,
∴∠APB=120°,
∴點P運動的路徑長是以AB為弦、圓周角∠APB=120°的弓形的弧長,
如圖2,∵∠APB=120°,
∴∠AOB=120°,
∴OB=$\frac{BH}{sin∠BOH}$=2$\sqrt{3}$,
點P運動的路徑長為:$\frac{120π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}}{3}π$.
點評 本題考查的是全等三角形的判定和性質、直角三角形的性質、點的軌跡的確定,掌握全等三角形的判定定理和性質定理、直角三角形的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | 3(x+1)2=2(x+1) | D. | x2-x(x+7)=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知等邊△ABC,M是邊BC延長線上一點,連接AM交△ABC的外接圓于點D,延長BD至N,使得BN=AM,連接CN,MN,解答下列問題:
已知等邊△ABC,M是邊BC延長線上一點,連接AM交△ABC的外接圓于點D,延長BD至N,使得BN=AM,連接CN,MN,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
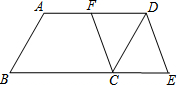 如圖,在?ABCD中,F是AD的中點,延長BC到點E,使CE=$\frac{1}{2}$BC,連接DE,CF.
如圖,在?ABCD中,F是AD的中點,延長BC到點E,使CE=$\frac{1}{2}$BC,連接DE,CF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com