
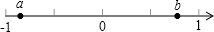 有兩個十分喜歡探究的同學小明和小芳,他們善于將所做的題目進行歸類,下面是他們的探究過程.
有兩個十分喜歡探究的同學小明和小芳,他們善于將所做的題目進行歸類,下面是他們的探究過程.分析 (1)根據要求填空即可;
(2)先根據數軸上點的位置確定:a<0,b>0,b>a,再根據(1)中的公式代入計算即可.
解答 解:(1)$\sqrt{2^2}$=2; $\sqrt{5^2}$=5; $\sqrt{6^2}$=6;$\sqrt{0^2}$=0; $\sqrt{{{({-3})}^2}}$=|-3|=3; $\sqrt{{{({-6})}^2}}$=|-6|=6;
故答案為:2,5,6,0,3,6;
②對于任意數a,有$\sqrt{a^2}$=|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$,
故答案為:|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$;
③$(\sqrt{4}{)^2}$=4; $(\sqrt{9}{)^2}$=9; $(\sqrt{25}{)^2}$=25;$(\sqrt{36}{)^2}$=36;$(\sqrt{49}{)^2}$=49; $(\sqrt{0}{)^2}$=0;
故答案為:4,9,25,36,49,0
④對于任意非負數a,有$(\sqrt{a}{)^2}$=a,
故答案為:a;
(2)由數軸得:a<0,b>0,b>a,
∴b-a>0
化簡:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$-$(\sqrt{b-a}{)^2}$.
=|a|-|b|+|a-b|-(b-a)
=-a-b+b-a-b+a
=-a-b.
點評 本題屬于閱讀理解問題,主要考查了算術平方根和平方的定義、數軸的知識,正確把握算術平方根定義是解題關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
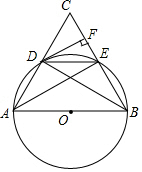 如圖,AB為⊙O的直徑,點C為圓外一點,連接AC、BC,分別與⊙O相交于點D、點E,且$\widehat{AD}$=$\widehat{DE}$,過點D作DF⊥BC于點F,連接BD、DE、AE.
如圖,AB為⊙O的直徑,點C為圓外一點,連接AC、BC,分別與⊙O相交于點D、點E,且$\widehat{AD}$=$\widehat{DE}$,過點D作DF⊥BC于點F,連接BD、DE、AE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖是一條河,A、B是對岸兩點(AB垂直河岸),某同學站在B點,在不能到達對岸的情況下,請你幫他設計至少兩種方案求出A、B之間的距離,并請說明理由.
如圖是一條河,A、B是對岸兩點(AB垂直河岸),某同學站在B點,在不能到達對岸的情況下,請你幫他設計至少兩種方案求出A、B之間的距離,并請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
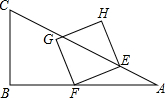 如圖,在△ABC中,∠B=90°,AB=4,BC=2,點E從點A出發,以每秒$\sqrt{5}$個單位長度的速度沿邊AC向終點C運動,E點出發的同時,點F從點B出發,以每秒2個單位長度的速度沿邊BA向終點A運動,連結EF,將線段EF繞點F逆時針旋轉90°得到線段FG,以EF、FG為邊作正方形EFGH,設點F運動的時間為t秒(t>0)
如圖,在△ABC中,∠B=90°,AB=4,BC=2,點E從點A出發,以每秒$\sqrt{5}$個單位長度的速度沿邊AC向終點C運動,E點出發的同時,點F從點B出發,以每秒2個單位長度的速度沿邊BA向終點A運動,連結EF,將線段EF繞點F逆時針旋轉90°得到線段FG,以EF、FG為邊作正方形EFGH,設點F運動的時間為t秒(t>0)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
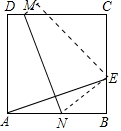 如圖,在正方形ABCD中,E是BC的中點,折疊正方形使點A與E重合,折痕為MN,若梯形ADMN的面積是$\frac{3}{2}$,則正方形的邊長是2;梯形ADMN與梯形BCMN的面積之比是$\frac{3}{5}$.
如圖,在正方形ABCD中,E是BC的中點,折疊正方形使點A與E重合,折痕為MN,若梯形ADMN的面積是$\frac{3}{2}$,則正方形的邊長是2;梯形ADMN與梯形BCMN的面積之比是$\frac{3}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
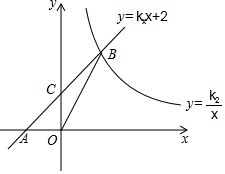 如圖,在平面直角坐標系中,一次函數y=k1x+2的圖象與x軸交于點A,與y軸交于點C,與反比例函數y=$\frac{{k}_{2}}{x}$的圖象在第一象限內交于點B,連結BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.
如圖,在平面直角坐標系中,一次函數y=k1x+2的圖象與x軸交于點A,與y軸交于點C,與反比例函數y=$\frac{{k}_{2}}{x}$的圖象在第一象限內交于點B,連結BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com