
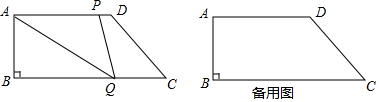
分析 (1)如圖1,作高線DE,證明四邊形ABED是矩形,再利用勾股定理求DC的長,在Rt△DEC中,求出
sin∠BCD=$\frac{DE}{DC}$=$\frac{4}{5}$;
(2)當四邊形PDCQ為平行四邊形時,點P在AD上,如圖2,根據PD=CQ列方程得:6-2t=t,解出即可;
(3)分三種情況:
①當0<t≤3時,點P在邊AD上,如圖3,直接利用面積公式求S即可;
②當3<t≤$\frac{11}{2}$時,點P在邊CD上,如圖4,利用梯形面積減去三個三角形面積的差求S;
③當$\frac{11}{2}$<t≤9時,點P與C重合,Q在BC上,如圖5,直接利用面積公式求S即可;
(4)畫出圖象,根據圖象得出結論.
解答 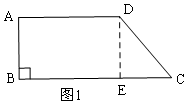 解:(1)過D作DE⊥BC于E,則∠BED=90°,
解:(1)過D作DE⊥BC于E,則∠BED=90°,
∵AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=90°,
∴∠B=∠BAD=90°,
∴四邊形ABED是矩形,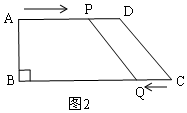
∴AD=BE=6,DE=AB=4,
∴EC=BC-BE=9-6=3,
在Rt△DEC中,由勾股定理得:DC=5,
sin∠BCD=$\frac{DE}{DC}$=$\frac{4}{5}$,
故答案為:5,$\frac{4}{5}$;
(2)由題意得:AP=2t,CQ=t,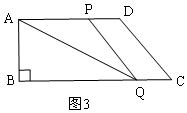
則PD=6-2t,
當四邊形PDCQ為平行四邊形時,如圖2,
則PD=CQ,
∴6-2t=t,
∴t=2;
(3)分三種情況:
①當0<t≤3時,點P在邊AD上,如圖3,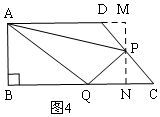
S=$\frac{1}{2}$AP•AB=$\frac{1}{2}$×4×2t=4t;
②當3<t≤$\frac{11}{2}$時,點P在邊CD上,如圖4,
過P作MN⊥BC,交BC于N,交AD的延長線于M,
由題意得:CQ=t,BQ=9-t,PA=2t,PD=2t-6,
∴PC=5-PD=5-(2t-6)=11-2t,
由圖1得:sin∠C=$\frac{4}{5}=\frac{PN}{PC}$,
$\frac{4}{5}=\frac{PN}{11-2t}$,
PN=$\frac{4(11-2t)}{5}$,
∴PM=4-PN=4-$\frac{4(11-2t)}{5}$=$\frac{4(2t-6)}{5}$,
S=S梯形ABCD-S△PQC-S△ABQ-S△APD,
=$\frac{(6+9)×4}{2}$-$\frac{1}{2}×6×\frac{4(2t-6)}{5}$-$\frac{1}{2}$×$t×\frac{4(11-2t)}{5}$-$\frac{1}{2}×(9-t)×4$=$\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}$;
③當$\frac{11}{2}$<t≤9時,點P與C重合,Q在BC上,如圖5,
S=$\frac{1}{2}×t×4$=2t;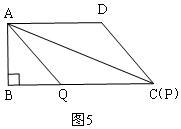
綜上所述,S與t的函數關系式為:S=$\left\{\begin{array}{l}{4t(0<t≤3)}\\{\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}(3<t≤\frac{11}{2})}\\{2t(\frac{11}{2}<t≤9)}\end{array}\right.$.
(4)如圖6,S=$\frac{4}{5}{t}^{2}-\frac{36}{5}t+\frac{132}{5}$;
S的最小值為:$\frac{4×\frac{4}{5}×\frac{132}{5}-(-\frac{36}{5})^{2}}{4×\frac{4}{5}}$=$\frac{51}{5}$,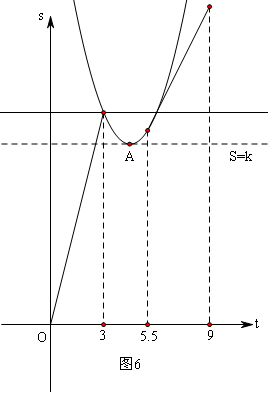
當t=3時,S=4×3=12,
∴則k的取值范圍是:$\frac{51}{5}$<k<12.
故答案為:$\frac{51}{5}$<k<12.
點評 本題是四邊形的綜合題,考查了梯形的性質、平行四邊形的性質、三角函數、面積的求法和函數問題,將四邊形與二次函數、一次函數相結合,綜合性較強,利用動點運動到不同位置,根據數形結合解決問題,本題還要注意點P運動結束后,點Q還繼續運動,即當$\frac{11}{2}$<t≤9時,點P與C重合,Q在BC上.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
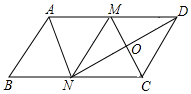 如圖,在?ABCD中,M,N分別是AD,BC的中點,∠AND=90°,連接CM交DN于點O.
如圖,在?ABCD中,M,N分別是AD,BC的中點,∠AND=90°,連接CM交DN于點O.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
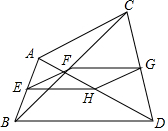 如圖,在四邊形ABDC中,E,F,G,H分別為AB,BC,CD,DA的中點,并且E,F,G,H四點不共線.
如圖,在四邊形ABDC中,E,F,G,H分別為AB,BC,CD,DA的中點,并且E,F,G,H四點不共線.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
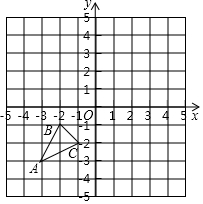 如圖,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐標系上三點.
如圖,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐標系上三點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
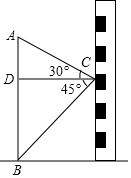 如圖在數學活動課中,小敏為了測量小院內旗桿AB的高度,站在教學樓上的C處測得旗桿低端B的俯角為45°,測得旗桿頂端A的仰角為30°,如旗桿與教學樓的水平距離CD為12m,則旗桿AB的高度是多少米?(參考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,結果精確到0.1米)
如圖在數學活動課中,小敏為了測量小院內旗桿AB的高度,站在教學樓上的C處測得旗桿低端B的俯角為45°,測得旗桿頂端A的仰角為30°,如旗桿與教學樓的水平距離CD為12m,則旗桿AB的高度是多少米?(參考值:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,結果精確到0.1米)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com