
 如圖所示,已知一長為2$\sqrt{3}$dm,寬為2dm的長方形木塊在桌面上做無滑動的翻滾,點A翻滾第一次到達點A1,翻滾到第二次時到達點A2,則點A經(jīng)過的路線與x軸和y軸圍成圖形的面積為(4$\sqrt{3}$+5π)dm2.
如圖所示,已知一長為2$\sqrt{3}$dm,寬為2dm的長方形木塊在桌面上做無滑動的翻滾,點A翻滾第一次到達點A1,翻滾到第二次時到達點A2,則點A經(jīng)過的路線與x軸和y軸圍成圖形的面積為(4$\sqrt{3}$+5π)dm2. 分析 根據(jù)勾股定理求得AB的長,依據(jù)點A經(jīng)過的路線與x軸和y軸圍成圖形的面積為S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$列式計算可得.
解答 解:∵AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,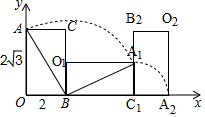
∴點A經(jīng)過的路線與x軸和y軸圍成圖形的面積為S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$
=$\frac{1}{2}$×2$\sqrt{3}$×2+$\frac{90•π•{4}^{2}}{360}$+$\frac{90•π•{2}^{2}}{360}$+$\frac{1}{2}$×2$\sqrt{3}$×2
=4$\sqrt{3}$+5π,
故答案為:(4$\sqrt{3}$+5π)dm2.
點評 本題主要考查軌跡和勾股定理、扇形的面積,根據(jù)題意畫出圖形得出點A經(jīng)過的路線與x軸和y軸圍成圖形的面積為S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$是解題的關鍵.


科目:初中數(shù)學 來源: 題型:解答題
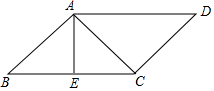 在?ABCD中,AC⊥CD,AE⊥BC.
在?ABCD中,AC⊥CD,AE⊥BC.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
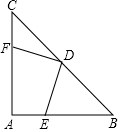 如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.
如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\sqrt{3+5}$=$\sqrt{3}$+$\sqrt{5}$ | B. | $\sqrt{3×5}$=$\sqrt{3}$×$\sqrt{5}$ | C. | $\frac{\sqrt{24}}{\sqrt{6}}$=$\sqrt{\frac{24}{6}}$ | D. | ($\sqrt{2}$)3=2$\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
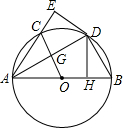 如圖,AB為⊙O的直徑,點D在⊙O上,DH⊥AB于H,現(xiàn)將△AHD沿AD翻折得到△AED,AE交⊙O于點C,連接OC交AD于點G.
如圖,AB為⊙O的直徑,點D在⊙O上,DH⊥AB于H,現(xiàn)將△AHD沿AD翻折得到△AED,AE交⊙O于點C,連接OC交AD于點G.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com