
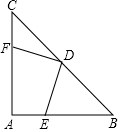
 如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.
如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.分析 (1)連接AD.只要證明△CDF≌△ADE(ASA)即可解決問題.
(2)連接EF,在RT△AEF中,求出FE,再根據等腰直角三角形的性質求出DE、DF即可解決問題.
解答 (1)證明:連接AD.
∵AB=AC,D為BC的中點,
∴AD⊥BC,
又∵∠BAC=90°,
∴AD=CD=BD,∠C=∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠ADE+∠ADF,
∴∠CDF=∠ADE,
在△CDF和△ADE中
$\left\{\begin{array}{l}∠C=∠DAE\\ CD=AD\\∠CDF=∠ADE\end{array}\right.$,
∴△CDF≌△ADE(ASA),
∴DF=DE.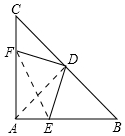
(2)連接EF.由(1)知,AE=CF=6,同理AF=BE=8
∵∠EAF=90°
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵DE=DF,DE⊥DF
∴△DEF為等腰三角形
∴DE2+DF2=EF2=100
∴DE=DF=5$\sqrt{2}$,
∴S△DEF=$\frac{1}{2}$•(5$\sqrt{2}$)2=25.
點評 本題考查等腰直角三角形的性質、全等三角形的判定和性質、勾股定理等知識,解題的關鍵是正確尋找全等三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖所示,已知一長為2$\sqrt{3}$dm,寬為2dm的長方形木塊在桌面上做無滑動的翻滾,點A翻滾第一次到達點A1,翻滾到第二次時到達點A2,則點A經過的路線與x軸和y軸圍成圖形的面積為(4$\sqrt{3}$+5π)dm2.
如圖所示,已知一長為2$\sqrt{3}$dm,寬為2dm的長方形木塊在桌面上做無滑動的翻滾,點A翻滾第一次到達點A1,翻滾到第二次時到達點A2,則點A經過的路線與x軸和y軸圍成圖形的面積為(4$\sqrt{3}$+5π)dm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 類型價格 | A型 | B型 |
| 進價(元/件) | 50 | 80 |
| 標價(元/件) | 80 | 120 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,點A、B、C的坐標分別為(-1,0)、(-2,3)、(-3,1).(1)作出△ABC關于x軸對稱的△A1B1C1,直接寫出B1、C1兩點的坐標:B1(-2,-3) C1(-3,-1).
在平面直角坐標系xOy中,點A、B、C的坐標分別為(-1,0)、(-2,3)、(-3,1).(1)作出△ABC關于x軸對稱的△A1B1C1,直接寫出B1、C1兩點的坐標:B1(-2,-3) C1(-3,-1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在扇形AOB中∠AOB=90°,正方形CDEF的頂點C是$\widehat{AB}$的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2$\sqrt{2}$時,求陰影部分的面積.
如圖,在扇形AOB中∠AOB=90°,正方形CDEF的頂點C是$\widehat{AB}$的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2$\sqrt{2}$時,求陰影部分的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com