
| 類型價格 | A型 | B型 |
| 進價(元/件) | 50 | 80 |
| 標價(元/件) | 80 | 120 |
分析 (1)設A型童裝購進x件,B型童裝購進y件,根據總價=單價×數量結合總利潤=單件利潤×數量即可得出關于x、y的二元一次方程組,解之即可得出結論;
(2)根據總利潤=A型童裝單件利潤×數量+B型童裝單件利潤×數量,代入數據即可得出結論.
解答 解:(1)設A型童裝購進x件,B型童裝購進y件,
根據題意得:$\left\{\begin{array}{l}{50x+80y=5400}\\{(80-50)x+(120-80)y=3000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=60}\\{y=30}\end{array}\right.$.
答:A型童裝購進60件,B型童裝購進30件.
(2)(80×0.8-50)×60+(120-80-30)×30=14×60+10×30=1140(元).
答:這批童裝全部售完后,童裝店共獲得1140元利潤.
點評 本題考查了二元一次方程組的應用,解題的關鍵是:(1)根據數量關系列出關于x、y的二元一次方程組;(2)根據數量關系列式計算.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
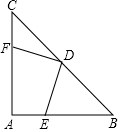 如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.
如圖,在等腰直角三角形ABC中,∠A=90°,AB=AC,點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且DE⊥DF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
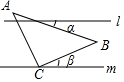 如圖,直線l∥m,等腰直角三角形ABC的直角頂點C在直線m上,若∠β=20°,則∠α的度數為( )
如圖,直線l∥m,等腰直角三角形ABC的直角頂點C在直線m上,若∠β=20°,則∠α的度數為( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{x-2}$ | B. | $\frac{2}{4x}$ | C. | $\frac{y-x}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-4x+4}{x-2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com