
分析 (1)由∠AOB=90°知∠BOC+∠AOC=90°、∠AOD+∠BOE=90°,根據(jù)∠AOD=∠AOC可得答案;
(2)①由∠COE=140°知∠COD=40°,分AB在直線DE上方和下方兩種情況,根據(jù)平行線的性質(zhì)分別求得∠AOD度數(shù),從而求得t的值;
②當(dāng)OA平分∠COD時∠AOD=∠AOC、當(dāng)OC平分∠AOD時∠AOC=∠COD、當(dāng)OD平分∠AOC時∠AOD=∠COD,分別列出關(guān)于t的方程,解之可得;
③由∠AOC=∠COE-∠AOE=140°-∠AOE、∠BOE=90°-∠AOE得∠AOC-∠BOE=(140°-∠AOE)-(90°-∠AOE)=50°.
解答 解:(1)∠BOC=∠BOE,
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,∠AOD+∠BOE=90°,
∵OA平分∠COD,
∴∠AOD=∠AOC,
∴∠BOC=∠BOE;
(2)①∵∠COE=140°,
∴∠COD=40°,
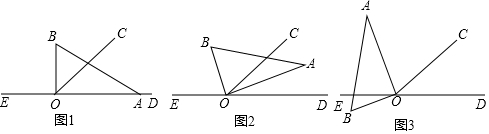
如圖1,當(dāng)AB在直線DE上方時,
∵AB∥OC,
∴∠AOC=∠A=30°,
∴∠AOD=∠AOC+∠COD=70°,即t=7;
如圖2,當(dāng)AB在直線DE下方時,
∵AB∥OC,
∴∠COB=∠B=60°,
∴∠BOD=∠BOC-∠COD=20°,
則∠AOD=90°+20°=110°,
∴t=$\frac{360°-110°}{10}$=25,
故答案為:7或25;
②當(dāng)OA平分∠COD時,∠AOD=∠AOC,即10t=20,解得t=2;
當(dāng)OC平分∠AOD時,∠AOC=∠COD,即10t-40=40,解得t=8;
當(dāng)OD平分∠AOC時,∠AOD=∠COD,即360-10t=40,解得:t=32;
綜上,t的值為2、8、32;
③∵∠AOC=∠COE-∠AOE=140°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOC-∠BOE=(140°-∠AOE)-(90°-∠AOE)=50°,
∴∠AOC-∠BOE的值為50°.
點(diǎn)評 本題主要考查平行線的性質(zhì)、角平分線的性質(zhì)、余角的性質(zhì)及角的計算,根據(jù)題意全面考慮所有可能以分類討論是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
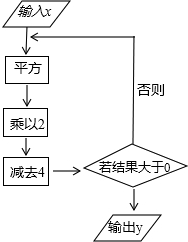 根據(jù)如圖所示的程序計算.
根據(jù)如圖所示的程序計算.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點(diǎn)M,若DM=1,求BC的值.
如圖,已知在等腰直角三角形ABC中,∠CAB=90°,以AB為邊向外作等邊△ABD,AE⊥BD,CD、AE交于點(diǎn)M,若DM=1,求BC的值.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在△ABC中,∠ACB=90°,AC=BC,點(diǎn)D為AB中點(diǎn),點(diǎn)E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.
如圖,在△ABC中,∠ACB=90°,AC=BC,點(diǎn)D為AB中點(diǎn),點(diǎn)E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2016-2017學(xué)年北京市西城區(qū)七年級上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:單選題
如圖所示,用量角器度量一些角的度數(shù)。下列結(jié)論中正確的是( )
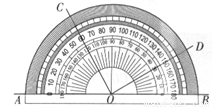
A. ∠BOC=60° B. ∠COD=150°
C. ∠AOC與∠BOD的大小相等 D. ∠AOC與∠BOD互余
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\root{3}{-27}$ | B. | -$\frac{5}{3}$ | C. | $\sqrt{0.01}$ | D. | 2π |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{x^2}{x^6}=\frac{1}{x^3}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a+b | ||
| C. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | D. | $\frac{x+1}{{x}^{2}-2x+1}$=$\frac{1}{x+1}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com