
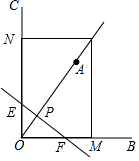
 如圖,∠BOC=90°,點(diǎn)A在∠BOC的內(nèi)部,OA=2,∠AOC=30°,點(diǎn)P,Q分別從點(diǎn)O,A同時(shí)出發(fā),均以每秒1個(gè)單位長度的速度沿OA方向運(yùn)動(dòng).過點(diǎn)P作直線l⊥OA于P,過點(diǎn)Q作QM⊥OB于點(diǎn)M,QN⊥OC于點(diǎn)N,設(shè)點(diǎn)P運(yùn)動(dòng)時(shí)間為t(s)
如圖,∠BOC=90°,點(diǎn)A在∠BOC的內(nèi)部,OA=2,∠AOC=30°,點(diǎn)P,Q分別從點(diǎn)O,A同時(shí)出發(fā),均以每秒1個(gè)單位長度的速度沿OA方向運(yùn)動(dòng).過點(diǎn)P作直線l⊥OA于P,過點(diǎn)Q作QM⊥OB于點(diǎn)M,QN⊥OC于點(diǎn)N,設(shè)點(diǎn)P運(yùn)動(dòng)時(shí)間為t(s)分析 (1)由題意OQ=OA+AQ=2+t,PO=t,即可推出PQ=OQ-OP=(2+t)-t=2.
(2)①如圖1中,當(dāng)點(diǎn)N與點(diǎn)F重合時(shí),在Rt△PQN中,由∠PQN=30°,PQ=2,推出PN=PQ•tan30°=$\frac{2}{3}$$\sqrt{3}$,在Rt△OPN中,OP=PN•tan30°=$\frac{2}{3}$,由此即可求出t的值.
②如圖2中,當(dāng)點(diǎn)M與點(diǎn)E重合時(shí).在Rt△PQM中,由∠PMQ=30°,PQ=2,推出PM=$\frac{PQ}{tan30°}$=2$\sqrt{3}$,在Rt△OPM中,OP=$\frac{PM}{tan30°}$=6,由此即求出t的值.
(3)分三種情形討論①如圖3中,當(dāng)0<t≤$\frac{2}{3}$時(shí),直線l掃過矩形QMON的圖形是△OMN.②如圖4中,$\frac{2}{3}$<t≤6時(shí),直線l掃過矩形QMON的圖形是四邊形MOFK.③如圖5中,當(dāng)t>6時(shí),直線l掃過矩形QMON的圖形是五邊形EOFKG.分別求解即可.
(4)分兩種情形①如圖6中,當(dāng)AF⊥ON時(shí).②如圖7中,當(dāng)AE⊥OM時(shí),分別求出OP的長即可解決問題.
解答 解:(1)由題意OQ=OA+AQ=2+t,PO=t,
∴PQ=OQ-OP=(2+t)-t=2.
∴OQ=2+t,PQ=2.
(2)①如圖1中,當(dāng)點(diǎn)N與點(diǎn)F重合時(shí).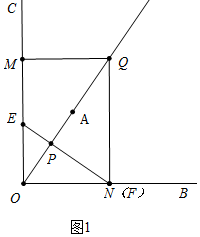
在Rt△PQN中,∵∠PQN=30°,PQ=2,
∴PN=PQ•tan30°=$\frac{2}{3}$$\sqrt{3}$,
在Rt△OPN中,OP=PN•tan30°=$\frac{2}{3}$,此時(shí)t=$\frac{2}{3}$s.
②如圖2中,當(dāng)點(diǎn)M與點(diǎn)E重合時(shí).
在Rt△PQM中,∵∠PMQ=30°,PQ=2,
∴PM=$\frac{PQ}{tan30°}$=2$\sqrt{3}$,
在Rt△OPM中,OP=$\frac{PM}{tan30°}$=6,
此時(shí)t=6s.
(3)①如圖3中,當(dāng)0<t≤$\frac{2}{3}$時(shí),直線l掃過矩形QMON的圖形是△OMN,易知ON=2t,OM=$\frac{2}{3}$$\sqrt{3}$t,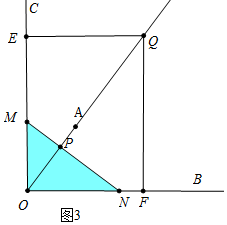
∴S=$\frac{1}{2}$•ON•OM=$\frac{2}{3}$$\sqrt{3}$t2.
②如圖4中,$\frac{2}{3}$<t≤6時(shí),直線l掃過矩形QMON的圖形是四邊形MOFK,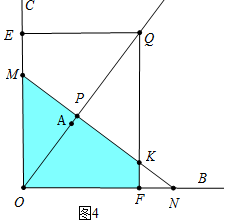
S=S△OMN-S△FKN=$\frac{2}{3}$$\sqrt{3}$t2-$\frac{1}{2}$•(2t-$\frac{t+2}{2}$)•$\frac{\sqrt{3}}{3}$(2t-$\frac{t+2}{2}$)=$\frac{7\sqrt{3}}{24}$t2+$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{6}$.
③如圖5中,當(dāng)t>6時(shí),直線l掃過矩形QMON的圖形是五邊形EOFKG.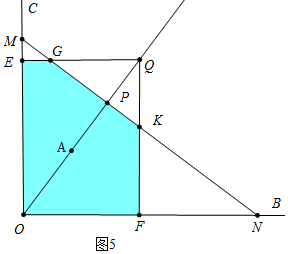
S=S△OMN-S△KFN-S△EGM=$\frac{7\sqrt{3}}{24}$t2+$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{6}$-$\frac{1}{2}$•[$\frac{2\sqrt{3}}{3}$t-(t+2)•$\frac{\sqrt{3}}{2}$]•$\sqrt{3}$•[$\frac{2\sqrt{3}}{3}$t-(t+2)•$\frac{\sqrt{3}}{2}$]=$\frac{\sqrt{3}}{4}$t2+$\sqrt{3}$t-$\frac{5\sqrt{3}}{3}$,
綜上所述,S=$\left\{\begin{array}{l}{\frac{2\sqrt{3}}{3}{t}^{2}}&{(0<t≤\frac{2}{3})}\\{\frac{7\sqrt{3}}{24}{t}^{2}+\frac{\sqrt{3}}{2}t-\frac{\sqrt{3}}{6}}&{(\frac{2}{3}<t≤6)}\\{\frac{\sqrt{3}}{4}{t}^{2}+\sqrt{3}t-\frac{5\sqrt{3}}{3}}&{(t>6)}\end{array}\right.$
(4)①如圖6中,當(dāng)AF⊥ON時(shí),
在Rt△OAF中,OF=OA•cos60°=1,
在Rt△OPF中,OP=$\frac{1}{2}$OF=$\frac{1}{2}$,此時(shí)t=$\frac{1}{2}$s.
②如圖7中,當(dāng)AE⊥OM時(shí),
在Rt△AEO中,OE=OA•cos30°=$\sqrt{3}$,
在Rt△OPE中,OP=OE•cos30°=$\frac{3}{2}$,
綜上所述,當(dāng)t為$\frac{1}{2}$s或$\frac{3}{2}$s時(shí),直線AE和直線AF這兩條直線的一條與矩形QMON的邊垂直.
點(diǎn)評 本題考查四邊形綜合題、矩形的性質(zhì)、銳角三角函數(shù)、三角形的面積以及路程、速度、時(shí)間之間的關(guān)系等知識,解題的關(guān)鍵是學(xué)會(huì)用分類討論的思想思考問題,學(xué)會(huì)利用分割法求多邊形的面積,屬于中考壓軸題.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知,如圖,等腰直角△ABC與等腰直角△CEF,∠ABC=∠CEF=90°,連結(jié)AF,M時(shí)AF的中點(diǎn),連結(jié)MB,且點(diǎn)C,B,E在同一直線上.求證:BM∥CF.
已知,如圖,等腰直角△ABC與等腰直角△CEF,∠ABC=∠CEF=90°,連結(jié)AF,M時(shí)AF的中點(diǎn),連結(jié)MB,且點(diǎn)C,B,E在同一直線上.求證:BM∥CF.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
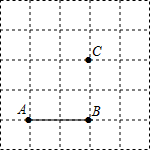 如圖,己知線段AB及點(diǎn)C,在方格紙上畫圖并回答問題.
如圖,己知線段AB及點(diǎn)C,在方格紙上畫圖并回答問題.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com