
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 不等式組變形后,根據無解確定出a的范圍,再表示出分式方程的解,由分式方程有整數解,確定出六個數中滿足條件a的值,進而求出之和.
解答 解:解$\left\{\begin{array}{l}{2(x+2)≤4+3x}\\{\frac{x+3}{2}<\frac{a+1}{2}-x}\end{array}\right.$,得$\left\{\begin{array}{l}{x≥0}\\{x<\frac{a-2}{3}}\end{array}\right.$,
∵不等式組$\left\{\begin{array}{l}{2(x+2)≤4+3x}\\{\frac{x+3}{2}<\frac{a+1}{2}-x}\end{array}\right.$ 無解,
∴$\frac{a-2}{3}$≤0,
∴a≤2.
解方程$\frac{ax-1}{x-1}$-1=$\frac{2}{1-x}$,得x=$\frac{2}{1-a}$,
∵x=$\frac{2}{1-a}$為整數,a≤2,
∴a=-1或0或2,
∵a=-1時,x=1,原分式方程無解,故將a=-1舍去,
∴所有滿足條件的a的值之和是0+2=2,
故選D.
點評 本題考查了解分式方程,解一元一次不等式組,熟練掌握解分式方程和一元一次不等式組的方法是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
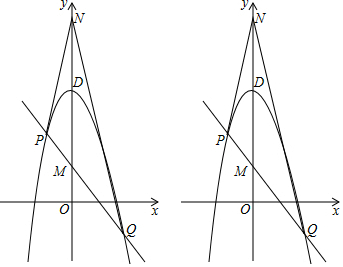
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
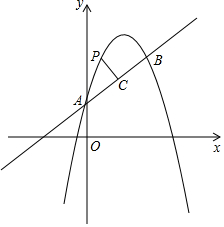 如圖,拋物線y=-x2+bx+c與直線y=$\frac{1}{2}$x+1交于A、B兩點,其中點A在y軸上,點B的橫坐標是4,P為拋物線上一動點,過點P作PC⊥AB,垂足為點C,設點P的橫坐標為m.
如圖,拋物線y=-x2+bx+c與直線y=$\frac{1}{2}$x+1交于A、B兩點,其中點A在y軸上,點B的橫坐標是4,P為拋物線上一動點,過點P作PC⊥AB,垂足為點C,設點P的橫坐標為m.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
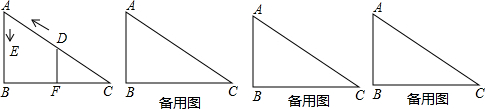
 如圖,在△ABC中,∠BAC=90°,AB=AC=3,點D在BC上且BD=2CD,E,F分別在AB,AC上運動且始終保持∠EDF=45°,設BE=x,CF=y,則y與x之間的函數關系用圖象表示為:( )
如圖,在△ABC中,∠BAC=90°,AB=AC=3,點D在BC上且BD=2CD,E,F分別在AB,AC上運動且始終保持∠EDF=45°,設BE=x,CF=y,則y與x之間的函數關系用圖象表示為:( )| A. | 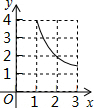 | B. | 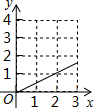 | C. | 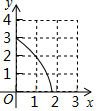 | D. | 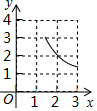 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com