
分析 首先根據題意畫出圖形,然后作OM⊥AB與M.根據垂徑定理和勾股定理求解.
解答 解:如圖,作OM⊥AB與M,
∵AB=8,
∴BM=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∵PB=3,
∴PM=1,P′M=7,
在直角△OBM中,OM=$\sqrt{O{B}^{2}-B{M}^{2}}$=3;
在Rt△OPM中,OP=$\sqrt{O{M}^{2}+P{M}^{2}}$=$\sqrt{10}$.
在Rt△OMP′中,OP′=$\sqrt{O{M}^{2}+MP{′}^{2}}$=$\sqrt{58}$.
∴OP=$\sqrt{10}$或OP=$\sqrt{58}$.
故答案是:$\sqrt{10}$或$\sqrt{58}$.
點評 此題考查了垂徑定理以及勾股定理.此題難度不大,注意掌握輔助線的作法,注意掌握數形結合思想與分類討論思想的應用.


科目:初中數學 來源: 題型:解答題
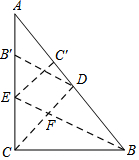 如圖,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折疊,使點B落在CA邊上的B'處,展開后,再沿BE折疊,使點C落在BA邊上的C'處,CD與BE交于點F.
如圖,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折疊,使點B落在CA邊上的B'處,展開后,再沿BE折疊,使點C落在BA邊上的C'處,CD與BE交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4,5,6 | B. | 1.5,2,2.5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com