Question

1．如圖，C是優弧AD的中點，DB⊥AC交圓O于點B，E是垂足．
（1）求證：∠ABD=2∠ADB；
（2）作OF⊥BD，F是垂足，求證：AB=2EF；
（3）在（2）的條件下，P是劣弧AD上一點，連接PD，若∠APD-∠PDB=90°，EF=$\frac{5}{2}$，DF=$\frac{11}{2}$，求AP的長．

Answer 1

分析 （1）如圖1中，連接CD，CO，延長CO交BD于N，交AD于M．只要證明∠1=∠2=∠3，∠B=∠ACD即可解決問題．
（2）如圖2中，作ON⊥AC于N，延長CO交⊙O于M，連接AM，CD．首先證明四邊形OFEN是矩形，推出ON=EF，再證明AM=2EF，AB=AM即可解決問題．
（3）如圖3中，連接CD，延長CA交DP的延長線于N．由題意可知AB=5，BE=3，AE=4，由△ABE∽△DCE，可得BE•DE=AE•EC，推出EC=$\frac{BE•DE}{AE}$=6，推出AC=CD=ND=10，EC=EN=6，AN=2，由△NAP∽△NDC，推出NA•NC=NP•ND，推出NP=$\frac{2×12}{10}$=$\frac{12}{5}$，由$\frac{AP}{DC}$=$\frac{NP}{NC}$，可得$\frac{AP}{10}$=$\frac{\frac{12}{5}}{12}$，即可求出AP．

解答 （1）證明：如圖1中，連接CD，CO，延長CO交BD于N，交AD于M．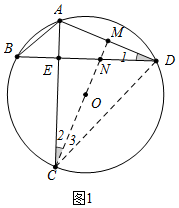

∵$\widehat{AC}$=$\widehat{CD}$，
∴AM⊥AD，AC=CD，∠2=∠3，
∵BD⊥AC，
∴∠CEN=∠NMD=90°，
∴∠1+∠MND=90°，∠2+∠CNE=90°，
∵∠DNM=∠ENC，
∴∠1=∠2=∠3，
∵∠B=∠ACD，
∴∠B=2∠1，即∠ABD=2∠ADB．

（2）證明：如圖2中，作ON⊥AC于N，延長CO交⊙O于M，連接AM，CD．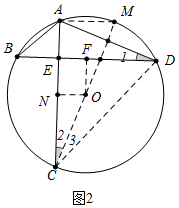

∵∠FEN=∠OFE=∠ONE=90°，
∴四邊形OFEN是矩形，
∴EF=ON，
∵ON⊥AC，
∴AN=CN，∵ON=OC，
∴AM=2ON=2EF，
∵∠1=∠2，
∴$\widehat{AB}$=$\widehat{AM}$，
∴AB=AM=2EF．

（3）解：如圖3中，連接CD，延長CA交DP的延長線于N．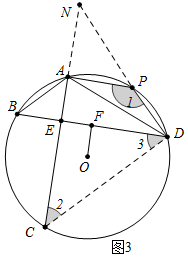

∵∠1+∠2=180°，∠1-∠PDB=90°，
∴∠2+∠PDB=90°，
∵∠2+∠3=90°，
∴∠3=∠PDB，
∵∠N+∠PDB=90°，
∴∠2=∠N，∴DN=DC，
∵EF=$\frac{5}{2}$，DF=$\frac{11}{2}$，
∴AB=2EF=5，
∵OF⊥BD，
∴BF=DF=$\frac{11}{2}$，
∴BE=BF-EF=3，
在Rt△ABE中，AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴△ABE∽△DCE，
∴BE•DE=AE•EC，
∴EC=$\frac{BE•DE}{AE}$=6，
∴AC=CD=ND=10，EC=EN=6，AN=2，
∵△NAP∽△NDC，
∴NA•NC=NP•ND，
∴NP=$\frac{2×12}{10}$=$\frac{12}{5}$，
∵$\frac{AP}{DC}$=$\frac{NP}{NC}$，
∴$\frac{AP}{10}$=$\frac{\frac{12}{5}}{12}$，
∴AP=2．

點評 本題考查圓綜合題、垂徑定理、等腰三角形的判定和性質、矩形的判定和性質．三角形的中位線定理、相似三角形的判定和性質、勾股定理等知識，解題的關鍵是學會添加常用輔助線，構造特殊四邊形解決問題，熟練掌握相似三角形的判定和性質，屬于中考壓軸題．