Question

4．如圖，在△ABC中，點D在△ABC的內部且DB=DC，點E，F在△ABC的外部，FB=FA，EA=EC，∠FBA=∠DBC=∠ECA．
（1）①填空：△ACE∽△ABF∽△BCD；
②求證：△CDE∽△CBA；
（2）求證：△FBD≌△EDC；
（3）若點D在∠BAC的平分線上，判斷四邊形AFDE的形狀，并說明理由．

Answer 1

分析 （1）①根據等腰三角形的性質得到∠DBC=∠DCB，∠FBA=∠FAB，∠ACE=∠EAC，等量代換得到∠FAB=∠BCD=∠EAC，于是得到結論；②根據相似三角形的性質得到$\frac{CE}{CA}=\frac{CD}{CB}$，根據相似三角形的判定定理即可得到結論；
（2）根據相似三角形的性質得到∠EDC=∠FBD，∠FDB=∠ACB等量代換得到∠FDB=∠ACB，根據全等三角形的判定即可得到結論；
（3）根據全等三角形的性質得到FB=DE，DF=CE，等量代換得到FD=AE，FA=DE，推出四邊形AFDE是平行四邊形，連接AD，于是得到AD平分∠BAC，根據菱形的判定定理即可得到結論．

解答 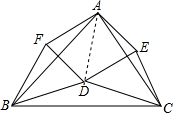解：（1）①∵DB=DC，
∴∠DBC=∠DCB，
∵FB=FA，EA=EC，
∴∠FBA=∠FAB，∠ACE=∠EAC，
∵∠FBA=∠DBC=∠ECA，
∴∠FAB=∠BCD=∠EAC，
∴△ACE∽△ABF∽△BCD；
故答案為：△ABF，△BCD；
②由①知，△ACE∽△BCD，
∴$\frac{CE}{CD}=\frac{CA}{CB}$，即$\frac{CE}{CA}=\frac{CD}{CB}$，
∵∠ECA=∠DCB，
∴∠ECD=∠ACB，
∴△CDE∽△CBA；

（2）∵△CDE∽△CBA，
∴∠ABC=∠EDC，
∵∠ABC=∠FBD，
∴∠EDC=∠FBD，
同理△BFD∽△BAC，
∴∠FDB=∠ACB，
∵∠ACB=∠ECD，
∴∠FDB=∠ACB，
在△FBD與△EDC中$\left\{\begin{array}{l}{∠FDB=∠ECD}\\{BD=CD}\\{∠FBD=∠EDC}\end{array}\right.$，
∴△FBD≌△EDC；

（3）四邊形AFDE是菱形，
理由：∵△FBD≌△EDC，
∴FB=DE，DF=CE，
∵FB=FA，EA=EC，
∴FD=AE，FA=DE，
∴四邊形AFDE是平行四邊形，
連接AD，則AD平分∠BAC，
即∠BAD=∠CAD，
∵∠BAF=∠CAE，
∴∠DAF=∠DAE，
∵AF∥DE，
∴∠DAF=∠ADE，
∴∠EAD=∠ADE，
∴EA=ED，
∴?AFDE是菱形．

點評 本題考查了相似三角形的判定和性質，全等三角形的判斷和性質，菱形的判定，平行四邊形的判定和性質，等腰三角形的性質，正確的理解題意是解題的關鍵．