
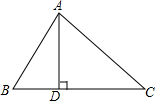
 如圖,在△ABC中,AD是BC邊上的高,∠B=45°,∠C=60°,AD=2,求BC的長.(結(jié)果保留根號)
如圖,在△ABC中,AD是BC邊上的高,∠B=45°,∠C=60°,AD=2,求BC的長.(結(jié)果保留根號) 分析 分別在RT△ABD和RT△ADC中根據(jù)勾股定理和等腰直角三角形的性質(zhì)求得BD、CD的長,則BC=BD+DC,由此其值就可以得到了.
解答 解:∵AD是BC邊上的高,∠C=60°,
∴∠CAD=30°,
∴CD=$\frac{1}{2}$AC,
在Rt△ACD中,根據(jù)勾股定理,
AC2-CD2=AD2,
(2CD)2-CD2=AD2,
∴CD=$\frac{{2\sqrt{3}}}{3}$,
∵AD是BC邊上的高,∠B=45°,
∴∠BAD=45°,
∴BD=AD=2,
∴BC=BD+CD=$2+\frac{{2\sqrt{3}}}{3}$.
點(diǎn)評 此題考查了勾股定理,求一般三角形的邊常用的方法就是作高,從而把一般三角形的問題轉(zhuǎn)化到直角三角形中進(jìn)行求解.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知AB為⊙O的直徑,點(diǎn)E在⊙O上,∠EAB的平分線交⊙O于點(diǎn)C,過點(diǎn)C作AE的垂線,垂足為D,直線DC與AB的延長線交于點(diǎn)P.
如圖,已知AB為⊙O的直徑,點(diǎn)E在⊙O上,∠EAB的平分線交⊙O于點(diǎn)C,過點(diǎn)C作AE的垂線,垂足為D,直線DC與AB的延長線交于點(diǎn)P.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
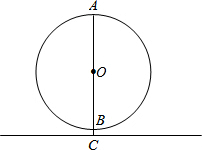 如圖,⊙O是夢幻谷的摩天輪示意圖,⊙O的最高處A到地面的距離是23米,最低處B到地面的距離是3米,AB是直徑,摩天輪勻速轉(zhuǎn)動,從B處乘坐繞摩天輪一周要6分鐘,
如圖,⊙O是夢幻谷的摩天輪示意圖,⊙O的最高處A到地面的距離是23米,最低處B到地面的距離是3米,AB是直徑,摩天輪勻速轉(zhuǎn)動,從B處乘坐繞摩天輪一周要6分鐘,查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖所示,兩個(gè)等腰三角形的頂角互補(bǔ),其中一個(gè)三角形的邊長是a,a,b(a>b),另一個(gè)三角形的邊長為b,b,a,則這兩個(gè)三角形的六個(gè)內(nèi)角中,度數(shù)最大的是( )
如圖所示,兩個(gè)等腰三角形的頂角互補(bǔ),其中一個(gè)三角形的邊長是a,a,b(a>b),另一個(gè)三角形的邊長為b,b,a,則這兩個(gè)三角形的六個(gè)內(nèi)角中,度數(shù)最大的是( )| A. | 75° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com